F = –kx
The minus sign shows that this force is in the opposite direction of the force that’s stretching or compressing the spring. The variables of the equation are F, which represents force, k, which is called the spring constant and measures how stiff and strong the spring is, and x, the distance the spring is stretched or compressed away from its equilibrium or rest position.
The force exerted by a spring is called a restoring force; it always acts to restore the spring toward equilibrium.
In Hooke’s law, the negative sign on the spring’s force means that the force exerted by the spring opposes the spring’s displacement.
Understanding springs and their direction of force
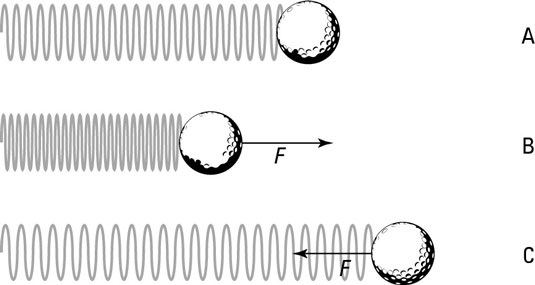
Hooke’s law is valid as long as the elastic material you’re dealing with stays elastic — that is, it stays within its elastic limit. If you pull a spring too far, it loses its stretchy ability. As long as a spring stays within its elastic limit, you can say that F = –kx.
When a spring stays within its elastic limit and obeys Hooke’s law, the spring is called an ideal spring.
How to find the spring constant (example problem)
Suppose that a group of car designers knocks on your door and asks whether you can help design a suspension system. “Sure,” you say. They inform you that the car will have a mass of 1,000 kilograms, and you have four shock absorbers, each 0.5 meters long, to work with. How strong do the springs have to be? Assuming these shock absorbers use springs, each one has to support a mass of at least 250 kilograms, which weighs the following:F = mg = (250 kg)(9.8 m/s2) = 2,450 N
where F equals force, m equals the mass of the object, and g equals the acceleration due to gravity, 9.8 meters per second2. The spring in the shock absorber will, at a minimum, have to give you 2,450 newtons of force at the maximum compression of 0.5 meters. What does this mean the spring constant should be?
In order to figure out how to calculate the spring constant, we must remember what Hooke’s law says:
F = –kx
Now, we need to rework the equation so that we are calculating for the missing metric, which is the spring constant, or k. Looking only at the magnitudes and therefore omitting the negative sign, you get
![]()
Time to plug in the numbers:
![]()
The springs used in the shock absorbers must have spring constants of at least 4,900 newtons per meter. The car designers rush out, ecstatic, but you call after them, “Don’t forget, you need to at least double that if you actually want your car to be able to handle potholes.”





