It’s a fact of life: You need to be able to do algebra to handle physics problems. Take the following equation, for example, which relates the distance something has traveled (s) to its acceleration and the time it has been accelerated:
Now suppose that the physics problem asks you for the acceleration, not the distance. You have to rearrange things a little here to solve for the acceleration. So when you multiply both sides by 2 and divide both sides by t2, here’s what you get:
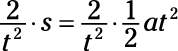
Cancelling out and swapping sides, you solve for a like this:
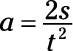
So that’s putting a little algebra to work. All you had to do was move variables around the equation to get what you wanted. The same approach works when solving physics problems (most of the time). On the other hand, what if you had to solve the same problem for the time, t? You would do that by rearranging the variables like so:
The lesson in this example is that you can extract all three variables — distance, acceleration, and time — from the original equation. Should you memorize all three versions of this equation? Of course not. You can just memorize the first version and use a little algebra to get the rest.
Sample question
-
The equation for final speed, vf — where the initial speed is v0, the acceleration is a, and the time is t — is vf = v0 + at. Solve for acceleration.
The correct answer is a = (vf – v0)/t
To solve for a, subtract v0 from both sides of the equation and then divide both sides of the equation by time, t.
Practice questions
-
The equation for potential energy, PE, for a mass m at height h, where the acceleration due to gravity is g, is PE = mgh. Solve for h.
-
The equation relating final speed, vf, to original speed, v0, in terms of acceleration a and distance s is vf2 = v02 + 2as. Solve for s.
-
The equation relating distance s to acceleration a, time t, and speed v is
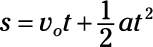
Solve for v0.
-
The equation for kinetic energy is
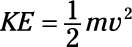
Solve for v.
Following are answers to the practice questions:
-
h = PE/mg
Divide both sides by mg to get your answer.
-
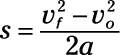
Divide both sides by 2a to get your answer.
-
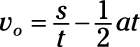
Subtract
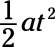
from both sides:
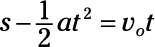
Divide both sides by t to get your answer.
-
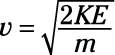
Multiply both sides by 2/m:
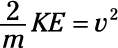
Take the square root to get your answer.

