In the sixth century B.C., the Greek scholar and philosopher Pythagoras decided to try to make things easier for everyone by standardizing, or at least dissecting, musical tuning. He had already discovered pitch frequencies in musical instruments by vibrating different lengths of string, and he had defined what exactly an octave was, so he figured this was the next logical step and created something that is now called the Pythagorean Circle, which eventually led to the more common Circle of Fifths.
Each of the 12 points around the circle was assigned a pitch value. This roughly corresponds to the present system of an octave with 12 half steps. So far, so good.
In mathematical terms, the unit of measure used in his Circle is cents, with 1,200 cents equal to one octave. Each half step, then, is broken up into 100 cents. Western music theorists have since updated Pythagoras's Circle, as shown in Figure 1.
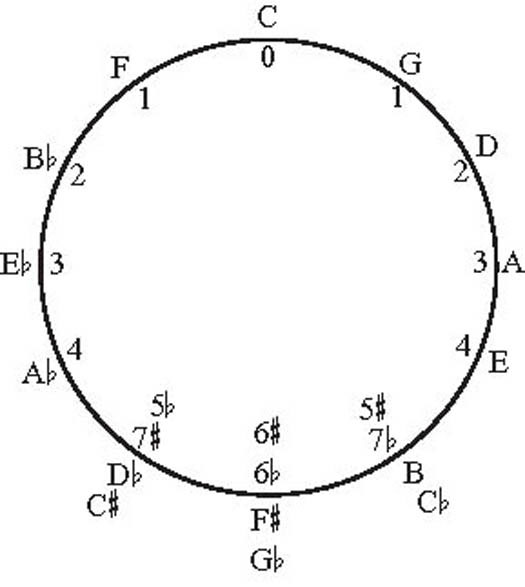
Figure 1: The Circle of Fifths is a foundational tool in Western music theory.
The creation and use of the Circle of Fifths is the very foundation of Western music theory. Along with all the technical things the Circle predicts, it's also your best friend in the world in deciphering key signatures on sight. It's just as essential in writing music because its clever design is very helpful in composing and harmonizing melodies, building chords, and moving to different keys within a composition.
Just as Pythagoras had it, the Circle of Fifths is divided up into 12 stops, like the numbers on a clock. Each stop is actually the fifth pitch in the scale of the preceding stop, which is why it's called the Circle of Fifths.
For example, the fifth pitch of the C scale is G. If you look at the Circle of Fifths in Figure 1, you'll see that G is the next letter to the right of C. If you keep going clockwise, you'll see that the fifth note of the G scale, D, is the next stop. And so on.
The Circle of Fifths helps you figure out which sharps and flats occur in what key. The name of the key being played is the letter on the outside of the Circle. To figure out how many sharps are in each key, count clockwise from C at the top of the Circle.
C major has a number value of 0, so that means it has no sharps. G has a value of 1, so it has one sharp. When you play the G major scale on the piano, you will find that you play only white keys until you come to the seventh interval and land on that one sharp: F sharp, in this case. D has two sharps, A has three, and so on around the Circle. The number value by each letter on the right-hand side of the Circle represents how many sharps are in that key.
To determine the number of flats in a key, go through the same process, but count counterclockwise. The key of E-flat major, therefore, has three flats.
You can also use the Circle of Fifths to figure out the key signature for minor keys. Starting with the key you want to use, just move three spaces counterclockwise and use the key signature for that major key. For example, to figure out the key signature for E minor, find E on the Circle of Fifths and move three spaces counterclockwise, which lands you on G. This tells you that E minor uses the same key signature as G major.
Major and minor keys that share a key signature are considered relatives. In this example, G is the relative major of E minor, and E is the relative minor of G major.






