Identities for angles that are twice as large as one of the common angles (double angles) are used frequently in trig. These identities allow you to deal with a larger angle in the terms of a smaller and more-manageable one.
A double-angle function is written, for example, as sin 2θ, cos 2α, or tan 2x, where 2θ, 2α, and 2x are the angle measures and the assumption is that you mean sin(2θ), cos(2α), or tan(2x). Because tangent is equal to the ratio of sine and cosine, its identity comes from their double-angle identities.
The double-angle identities find the function for twice the angle θ. Note that the cosine function has three different versions of its double-angle identity.
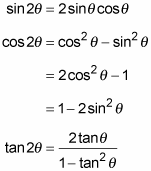
Finding the cosine of twice an angle is easier than finding the other function values, because you have three versions to choose from. You make your choice depending on what information is available and what looks easiest to compute. To show you where the first of the double-angle identities for cosine comes from, this example uses the angle-sum identity for cosine. Because the two angles are equal, you can replace β with α, so cos (α + β) = cosα cosβ – sin sinβ becomes
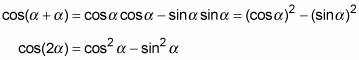
To get the second version, use the first Pythagorean identity, sin2 + cos2 = 1. Solving for sin2, you get sin2 = 1 – cos2. Putting this result back into the double-angle identity for cosine and simplifying, you get
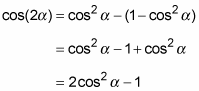
To find the last version of the double-angle identity for cosine, solve the first Pythagorean identity for cos2α, which gives you cos2α = 1 – sin2α. Then substitute this result into the first angle-sum identity for cosine:
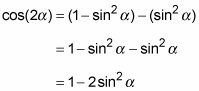
The biggest advantage to having three different identities for the cosine of a double angle is that you can solve for the cosine with just one other function value. The sum and difference identities for sine and cosine, on the other hand, as well as the double-angle identity for sine, all involve both the sine and cosine of the angles.
Here’s an example showing off that advantage. Find cos 2α; the angle α is in the fourth quadrant, and sinα = –0.45.
Choose the appropriate double-angle identity.
Because you know the value of the sine, use cos 2α = 1 – 2sin2α.
Insert the given value in the formula and simplify.

The resulting cosine is positive. The cosine is positive in the first and fourth quadrants, so how do you know which of those two quadrants the terminal side of this double angle lies in? Go back to the beginning of the problem — you know that the original angle is in the fourth quadrant. An angle in the fourth quadrant measures between 270 degrees and 360 degrees. If you double those numbers (because you’re working with a double angle), you get 540 degrees and 720 degrees. The angles between those two values lie in the third and fourth quadrants. The cosine is positive in the fourth quadrant, so this double angle lies in the fourth quadrant.





