When you know the values for two or more sides of a triangle, you can use the law of cosines. In the following case, you know all three sides (which is called SSS, or side-side-side, in trigonometry) but none of the angles. What you see here is how to solve for the measures of the three angles in triangle ABC, which has sides where a is 7, b is 8, and c is 2.
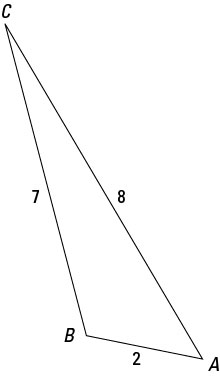
As you can see in the preceding figure, the triangle appears to have two acute angles and one obtuse angle, the obtuse angle being opposite the longest side.
Solve for the measure of angle A.
Using the law of cosines where side a is on the left of the equation, substitute the values that you know and simplify the equation.

Now use a scientific calculator to find the measure of A.
A = cos–1(0.594) = 53.559
Angle A measures about 54 degrees.
Solve for the measure of angle B.
Using the law of cosines where side b is on the left of the equation, input the values that you know and simplify the equation.

The negative cosine means that the angle is obtuse — its terminal side is in the second quadrant. Now use a scientific calculator to find the measure of B.
B = cos–1(–0.393) = 113.141
Angle B measures about 113 degrees.
Determine the measure of angle C.
Because angle A measures 54 degrees and angle B measures 113 degrees, add them together and subtract the sum from 180 to get the measure of angle C.
180 – (54 + 113) = 180 – 167 = 13. Angle C measures only 13 degrees.





