The Law of Cosines works well for solving triangles when you have two sides and an angle, but the angle isn’t between the two sides. In this case, the Law of Sines isn’t an option. Also, to solve a triangle that is SSA (or side-side-angle) using the Law of Cosines, you have to be careful to find the correct triangle — there are two possibilities.
Drawing a picture helps explain why the situation may have more than one answer. When you use this setup in an actual application, the correct answer is usually pretty clear.
The situation is that you know the measures of two of the sides to be 93 and 85 units. The angle opposite the side measuring 85 has a measure of 61 degrees. You see two ways of drawing the corresponding picture.
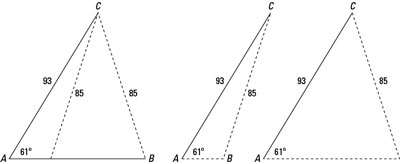
Find the missing parts of the triangle ABC that has sides a and b measuring 85 and 93, respectively, and angle A measuring 61 degrees. The preceding figure presents the situation.
Find the length of side c by using the law of cosines with a on the left-hand side of the equation.
Use this form because after you input the known values, it’s the only one that will have just one variable to solve for — even though that variable has two powers.
Enter the values into the law of cosines.
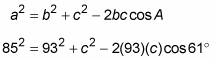
Simplify the equation by performing all the operations and getting the variables alone on the right side.
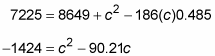
You end up with a quadratic equation.
Use either the quadratic formula or a calculator to determine the solutions.
0 = c2 – 90.21c + 1424
c = 69.813 or 20.397
So c measures either about 70 or about 20.
Let c measure 70, and find the measures of the other two angles.
This time, take a departure from the law of cosines and use, instead, the law of sines.
Use angle A and side a, and pair the ratio with angle C and side c to get
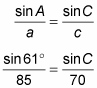
Now multiply each side by 70, and solve for the sine of C.
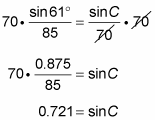
Solve for the angle with that sine.
C = sin–1(0.721) = 46.137
The measure of angle C is about 46 degrees.
If angle A is 61 degrees and angle C is 46 degrees, then angle B is 180 degrees minus the sum of A and C: 180 – (61 + 46) = 180 – 107 = 73 degrees.
Now let c measure 20, and find the measures of the other two angles.
Go back to the law of cosines to do this part. You can compare the two methods — the one in this step and the one in Step 2 — to see which one you like better.
Use the law with c on the left-hand side of the equation to solve for the cosine of angle C.

Use a calculator to find the measure of angle C.
C = cos–1(0.979) = 11.763°
Angle C measures about 12 degrees, which means that angle B is 180 – (61 + 12) = 180 – 73 = 107 degrees.
The ambiguous case causes a bit of confusion. Why would you want two answers? The following example may help clear up this mystery. You really don’t want two answers. You just want the one that answers your question.
Slim and Jim are both sitting at the intersection of two roads, which forms a 50-degree angle. They leave the intersection at the same time — Slim in his old, slow, beat-up pickup truck, and Jim in his nifty-swifty Jeep. When Jim was 400 yards down the road, the two of them were 320 yards apart. How far had Slim driven at that point?
You definitely need a picture for this problem, so:
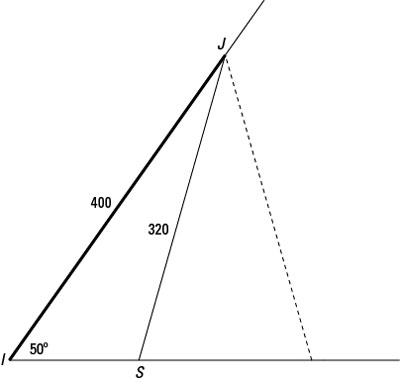
You can safely assume that Slim couldn’t have gone farther than Jim in his old clunker — unless his truck had hidden powers. Figure out how far Slim drove, the distance from I to S (this example refers to the distance as j to be consistent with the triangle labels) by using the law of cosines. The side s is 400 yards, and angle I is 50 degrees.
Write the law of cosines, and replace the letters with the values.
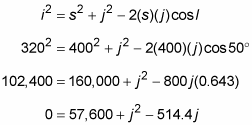
This equation simplifies to a quadratic equation with the variable j.
Solve the quadratic equation.
0 = j2 – 514.4j + 57,600
Use a calculator or the quadratic formula, and you get two solutions: x = 349.676 and x = 164.723. Either answer gives you a distance smaller than the distance that Jim traveled. Refer to the preceding figure, and choose the answer that appears to be correct, based on what you know.

