Familiarizing yourself with the different versions of Pythagorean identities is helpful so that you can easily recognize them when solving trigonometry equations or simplifying expressions.
All these different versions have their places in trigonometric applications, calculus, or other math topics. You don’t have to memorize them, because if you just remember the three Pythagorean identities, you can solve for what you need.
Changing sin2θ + cos2θ = 1
You can alter the original Pythagorean identity in myriad ways. For starters, you can isolate either sin2θ or cos2θ on one side of the equation by subtracting the other term:
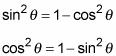
Continuing on, you can factor the right side of either of these equations because that side is the difference of two perfect squares:
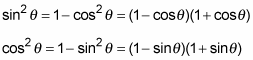
Sometimes, however, having an expression for sinθ or cosθ, where the functions aren’t squared, is helpful. Beginning with the basic Pythagorean identity, where one function is by itself, you can take the square root of each side to get
Adjusting tan2θ + 1 = sec2θ
You can also adapt this second Pythagorean identity in various ways. Solving for tan2θ by subtracting 1 from each side of the equation, you get
Then, factoring the difference of the squares on the right (because that side is the difference of two perfect squares), you have
Lastly, beginning with the earlier version and taking the square root of each side, you get
Taking another approach to this Pythagorean identity, you can subtract tan2 from each side and factor the result to get
Reconfiguring 1 + cot2θ = csc2θ
You can rearrange the last Pythagorean identity, too, by subtracting 1 from each side or by subtracting cot2θ from each side. The two new versions are
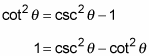
Each of the preceding equations has the difference of two perfect squares, which you can factor:
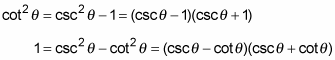
And lastly, the square root of each side yields an identity involving just cotθ:

