The easiest way to work with inverse trig functions is to have a chart handy with the exact values of the functions. When angles other than the most common or popular are involved, you can either use a table or get out your handy-dandy scientific calculator.
When you work with trigonometry a lot, you soon have the basic angles and their function values memorized. You also know that the sine and its reciprocal are positive in QI and QII; the cosine and its reciprocal are positive in QI and QIV; and the tangent and its reciprocal are positive in QI and QIII. Armed with the basics, you can come up with function values rather quickly and efficiently — without resorting to chart or calculator.
This first example uses the exact value from a chart (or from memory). Find
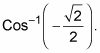
Determine the reference angle that you need by using the absolute value of the input.

Use the sign of the input to determine the correct quadrant.
Because

is negative, and of the two quadrants for the range, the cosine is negative in QII, the answer is an angle in QII whose reference angle is 45 degrees.
Determine the correct angle measure.
The angle in standard position in QII whose reference angle is 45 degrees is

The next example involves inverse cotangent. Find
Determine the reference angle that you need.

Use the sign of the input to determine the correct quadrant.

Determine the correct angle measure.
All angles in QI are the same as their reference angles, so

The problems that you encounter won’t always involve nice numbers from the most common angles. When you’re faced with a nasty little decimal value, you may have to use a table. In this next example, you start off with a decimal value, and an answer to the nearer degree is the proper response. The decimal in the following example is rounded off to three decimal places. To do these problems, you find the closest answer.
Find Arctan(–3.732).
Determine the reference angle that you need.
By using a table, you can see that the value 3.732 corresponds to the tangent of a 75-degree angle. This angle is the closest in whole degrees to having a tangent of 3.732.
Use the sign of the input to determine the correct quadrant.
Because –3.732 is negative, the answer is an angle in QIV whose reference angle is 75 degrees.
Determine the correct angle measure.
In QIV, a reference angle of 75 degrees has a measure of either –75 degrees or its positive equivalent (same terminal side), 285 degrees. So Arctan(–3.732) = Tan–1(–3.732) = –75° or 285°.





