When you already know two angles in a triangle as well as one of the sides, such as in the case of ASA or AAS, you can use the law of sines to find the measures of the other two sides. This law uses the ratios of the sides of a triangle and their opposite angles. The bigger the side, the bigger its opposite angle. The longest side is always opposite the largest angle. Here’s how it goes.
The law of sines for triangle ABC with sides a, b, and c opposite those angles, respectively, says
So the law of sines says that in a single triangle, the ratio of each side to its corresponding opposite angle is equal to the ratio of any other side to its corresponding angle.
For example, consider a triangle where side a is 86 inches long and angles A and B are 84 and 58 degrees, respectively. The following figure shows a picture of the triangle, and the following steps show you how to find the missing three parts.
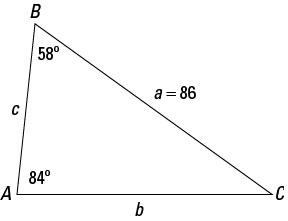
Find the measure of angle C.
The sum of the measures of a triangle’s angles is 180 degrees. So find the sum of angles A and B, and subtract that sum from 180.
180 – (84 + 58) = 180 – 142 = 38
Angle C measures 38 degrees.
Find the measure of side b.
Using the law of sines and the proportion
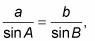
fill in the values that you know.
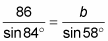
Use the given values, not those that you’ve determined yourself. That way, if you make an error, you can spot it easier later.
Use a calculator to determine the values of the sines (in this case, rounded to three decimal places).
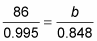
Multiply each side by the denominator under b to solve for that length. Because the original measures are whole numbers, round this answer to the nearer whole number.
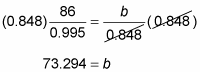
Side b measures about 73 inches.
Find the measure of side c.
Using the law of sines and the proportion
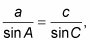
fill in the values that you know.
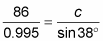
Again, it’s best to use the given values, not those that you determined. In this case, however, you have to use a computed value, the angle C.
Use a calculator to determine the values of the sines.
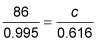
Multiply each side by the denominator under c to solve for that length. Because the original measures were given as whole numbers, round this answer to the nearer whole number.
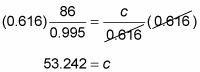
Side c measures about 53 inches.

