The graph for a secant function is different from the cosecant in several ways, but one of the most obvious ways is that the graph of the secant is symmetric about the y-axis. The secant is a mirror reflection over that axis. You can use this property to do something interesting to the graph.
The usual translations and multiplications affect the secant graph in the same way it does the graphs of the other trig functions. If you multiply the function by 1/6 and add 2π to the angle variable, as in the equation
you get this figure.
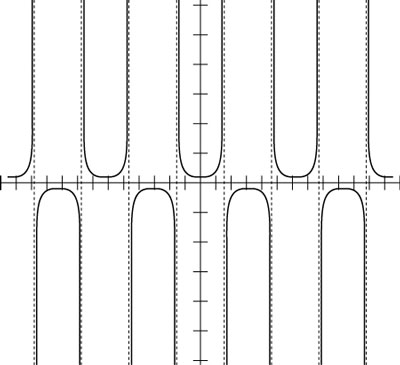
Compared to y = sec x, the graph in the preceding figure is much closer to the x-axis and seems to be flattened out between the asymptotes. These changes happen when you multiply the function by a number between 0 and 1. The turning point is still in the same place, but the y-value is much closer to 0.
The other curiosity is that the asymptotes don’t seem to be different. They aren’t — and they shouldn’t be. By adding 2π to the angle variable, you shift the graph 2π units to the left. The graph really has shifted, but you can’t tell, because the new graph lies completely on the old one. When the shift is equal to the period of the function (the length of the interval that it takes for the function values to start repeating over again), the change isn’t apparent.





