The graphs of the inverse secant and inverse cosecant functions will take a little explaining. First, keep in mind that the secant and cosecant functions don’t have any output values (y-values) between –1 and 1, so a wide-open space plops itself in the middle of the graphs of the two functions, between y = –1 and y = 1.
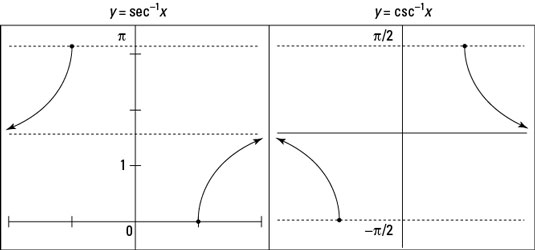
This situation translates into a wide-open space between the x-values –1 and 1 in the graphs of their inverses. Also, the graphs of secant and cosecant go infinitely high and infinitely low along the y-axis. So the graphs of the inverses have horizontal asymptotes. All this talk probably seems like nonsense, so take a look at the preceding figure, which shows the graphs.
The graph of y = sec–1 x lies between 0 and π on the y-axis. All the output values are in the first and second quadrants. But a horizontal asymptote runs through the graph:
output value there. The graph of the inverse secant goes from the point (1,0) and moves upward, staying below the horizontal asymptote as the x-values go to positive infinity. It also comes from negative infinity along the x-axis above the horizontal asymptote, moving upward to the point (–1,π).
The graph of y = csc–1 x lies between
with a horizontal asymptote of y = 0. (The cosecant isn’t defined at x = 0, so its inverse doesn’t have an output value there.) The graph of inverse cosecant covers angle measures from the first and fourth quadrants. On the right, the graph goes from the point
down toward the horizontal asymptote as the x-values go to positive infinity. On the left, the graph’s x-values come from negative infinity, where they’re just below the asymptote, and move down to the point

