You can use the graph of a trigonometry function to plot your biorhythm cycles. Many years ago, the public showed great interest in a person’s biorhythms, which are supposed to be the physical, emotional, and intellectual cycles that a person experiences in life.
Many people even wrote books about biorythms. And some believe that these cycles affect how a person reacts to situations in his or her life. They even go so far as to say that the positions of these curves influence major decisions of famous movie stars and politicians.
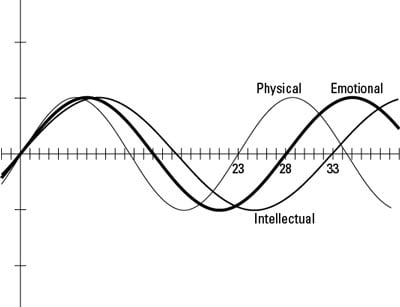
What do biorhythms have to do with trigonometry? Everything! This biorhythm theory uses the sine curve. Supposedly, our life cycles start at birth and fluctuate like sine curves. The physical cycle is 23 days long, the emotional cycle is 28 days long, and the intellectual cycle is 33 days long. These numbers translate into the periods of the respective cycles. If you plot all these cycles on a graph, starting on the day you were born, you can see where these cycles are right now and what they’ll look like in the future. The above figure shows a graph of the three biorhythm cycles.
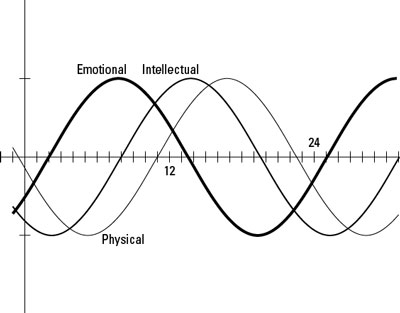
In the preceding figure, you can see, again, how the different cycles have different periods. Imagine these sine curves going on for years and years, crossing over the x-axis and over one another. The figure shows some biorhythm cycles plotted for some imaginary person for some year in the month of March.
If you believe in the biorhythm theory that says these curves exist, you can see that on the 12th of the month, all the cycles are above the x-axis, and on the 24th, they’re all below the x-axis. Supposedly, when a curve is above the x-axis, everything is bright and sunny — a person is in good health, emotionally fine, and very smart and with it. When the curve is below the x-axis, he or she tends to be sick, depressed, and dull. In addition, the theory says that when the cycles cross from above to below the axis, or vice versa, those days are critical. A critical day is when upheaval and crises are possible. Such a day is a good time to stay in bed — if that’s even safe. There’s no way to prove or disprove this theory, but it sure makes interesting use of the sine curve!

