The period of a trigonometry function is the extent of input values it takes for the function to run through all the possible values and start all over again in the same place to repeat the process. In the case of the function y = sin x, the period is 2π, or 360 degrees. Pick any place on the sine curve, follow the curve to the right or left, and 2π or 360 units from your starting point along the x-axis, the curve starts the same pattern over again.
Multiplying the angle variable, x, by a number changes the period of the sine function. If you multiply the angle variable by 3, such as in y = sin 3x, then the curve will make three times as many completions in the usual amount of space. So multiplying by 3 actually reduces the length of the period. In the case of
only half of the curve fits in the same space. So a coefficient less than 1 increases the number of inputs that the function needs to complete a cycle.
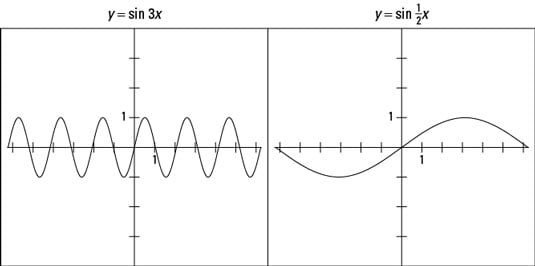
The preceding figure shows the graphs of y = sin 3x and
The location of the multiplier makes a big difference. Multiplying the sine function by 4 and its angle variable by 4 results in two completely different graphs. The graph of y = 4sin x is much higher than usual — the amplitude is greater than that of the standard sine function. The graph of y = sin 4x has an amplitude of 1, but the period is smaller and the curve is more scrunched together — it repeats over and over more quickly.

