The practice questions here have you working on margin of error for population means and population proportions. Solve the following problems related to margin of error and population proportion.
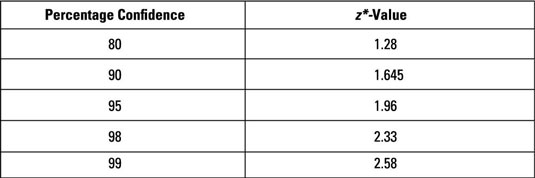
The following table provides the z*- values for selected (percentage) confidence levels.
Sample questions
A market researcher samples 100 people to find a confidence interval for estimating the average age of their customers. She finds that the margin of error is three times larger than she wants it to be.
How many people should the researcher add to the sample to bring the margin of error down to the desired size?
Answer: 800
The sample size, n, appears in the denominator of the formula for margin of error.

The researcher wants to cut the MOE to 1/3 of its current value, which is equivalent to dividing by 3. To retain the integrity of the equation, you must divide both sides by 3. Note that the denominator of the right-hand side of the equation is the square root of n; dividing by the square root of 9 is equivalent to dividing by 3, because 3 is the square root of 9.
So to divide the MOE by 3, holding everything else constant, you must increase the sample size to 9 times its current value.

Note that, because of the distributive law, the following is true:

Because n = 100 and 9n = (9)(100) = 900, the market researcher needs 800 more participants to get the desired margin of error (a total of 900 participants is required).
A survey of 10,000 randomly selected adults from across Europe finds that 53% are unhappy with the euro.
What is the margin of error for estimating the proportion among all Europeans who are dissatisfied with the euro? (Use a confidence level of 95%.) Give your answer as a percentage.
Answer: plus/minus 0.978%
The formula to calculate the margin of error (MOE) for a population proportion is

where z* is the value from the table for a given confidence level (95% in this case, or 1.96),

is the sample proportion (0.53), and n is the sample size (10,000).
You convert 53% to the proportion 0.53 by dividing the percentage by 100: 53/100 = 0.53.
Now, substitute the known values in the formula and solve:

Convert this proportion to a percentage by multiplying by 100%: (0.00978)(100%) = 0.978%
The margin of error is therefore plus/minus 0.978%.
You estimate that 53% plus/minus 0.978% of all Europeans are unhappy with the euro, based on these survey results with 95% confidence.
If you need more practice on this and other topics from your statistics course, visit 1,001 Statistics Practice Problems For Dummies to purchase online access to 1,001 statistics practice problems! We can help you track your performance, see where you need to study, and create customized problem sets to master your stats skills.





