A geometry proof — like any mathematical proof — is an argument that begins with known facts, proceeds from there through a series of logical deductions, and ends with the thing you’re trying to prove.
Geometry proofs follow a series of intermediate conclusions that lead to a final conclusion: Beginning with some given facts, say A and B, you go on to say therefore, C; then therefore, D; then therefore, E; and so on till you get to your final conclusion.
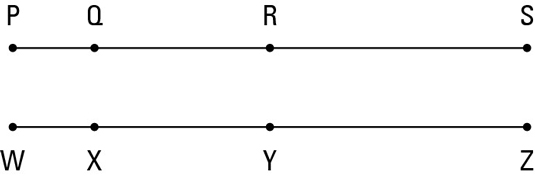
Here’s a very simple example using the line segments in the above figure.

And of course, you’d be right. But that’s not how the proof game is played. You have to spell out every little step in your thinking so your argument doesn’t have any gaps. Here’s the whole chain of logical deductions:






