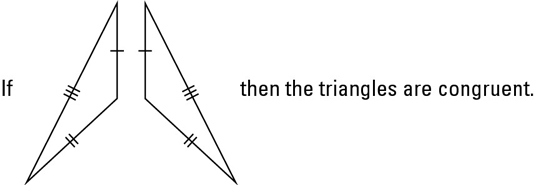
The SSS (Side-Side-Side) postulate states that if the three sides of one triangle are congruent to the three sides of another triangle, then the triangles are congruent. The following figure illustrates this idea.
You can use the SSS postulate in the following “TRIANGLE” proof (see diagram below):

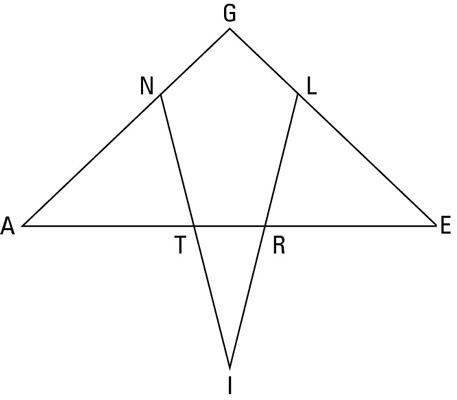
Before you begin writing a formal proof, figure out your game plan. Here’s how that might work.
You know you’ve got to prove the triangles congruent, so your first question should be “Can you show that the three pairs of corresponding sides are congruent?” Sure, you can do that:

To make the game plan more tangible, you may want to make up lengths for the various segments. For instance, say AG and EG are 9, NG and LG are 3, AR and ET are 8, TR is 3, and NI and LI are 8. When you do the math, you see that triangle ANT and triangle ELR both end up with sides of 4, 5, and 6, which means, of course, that they’re congruent.
Here’s how the formal proof shapes up:
Statement 1:
Reason for statement 1: Given.
Statement 2:
Reason for statement 2: If two congruent segments are subtracted from two other congruent segments, then the differences are congruent.
Statement 3:
Reason for statement 3: Given.
Statement 4:
Reason for statement 4: If a segment is subtracted from two congruent segments, then the differences are congruent.
Statement 5:

Reason for statement 5: Given.
Statement 6:
Reason for statement 6: If segments are congruent, then their Like Divisions are congruent (half of one equals half of the other).
Statement 7:
Reason for statement 7: SSS (using lines 2, 4, and 6).





