In an indirect geometric proof, you assume the opposite of what needs to be proven is true. Therefore, when the proof contradicts itself, it proves that the opposite must be true.
Practice questions
Use the following figure to answer the questions regarding this indirect proof.
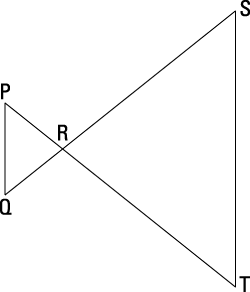
Given:
are straight lines.
Prove:
do not bisect each other.

What is the statement for Reason 2?
What is the reason for Statement 3?
What is the statement for Reason 4?
What is the reason for Statement 5?
What is the reason for Statement 6?
What is the reason for Statement 7?
What is the reason for Statement 8?
Answers and explanations
-

bisect each other.
In an indirect proof, assume the opposite of what needs to be proven is true.
A bisector divides a segment into two congruent segments.
-

are vertical angles.
Intersecting lines form vertical angles.
If two angles are vertical angles, then they're congruent.
SAS
If two sides and the included angle of one triangle are congruent to two sides and the included angle of another triangle, then the triangles are congruent by SAS (side-angle-side).
CPCTC
Corresponding parts of congruent triangles are congruent to each other.
Contradiction
Step 7 contradicts Step 1; therefore, the opposite must be true.





