- Arc: An arc is simply a curved piece of a circle. Any two points on a circle divide the circle into two arcs: a minor arc (the smaller piece) and a major arc (the larger)—unless the points are the endpoints of a diameter, in which case both arcs are semicircles.

Note that to name a minor arc, you use its two endpoints; to name a major arc, you use its two endpoints plus any point along the arc.
- Central angle: A central angle is an angle whose vertex is at the center of a circle. The two sides of a central angle are radii that hit the circle at the opposite ends of an arc—or as mathematicians say, the angle intercepts the arc.
The measure of an arc is the same as the degree measure of the central angle that intercepts it.
Determining the length of an arc
An arc’s length means the same commonsense thing length always means — you know, like the length of a piece of string (with an arc, of course, it’d be a curved piece of string). Make sure you don’t mix up arc length with the measure of an arc which is the degree size of its central angle.A circle is 360° all the way around; therefore, if you divide an arc’s degree measure by 360°, you find the fraction of the circle’s circumference that the arc makes up. Then, if you multiply the length all the way around the circle (the circle’s circumference) by that fraction, you get the length along the arc. So finally, here’s the formula you’ve been waiting for.
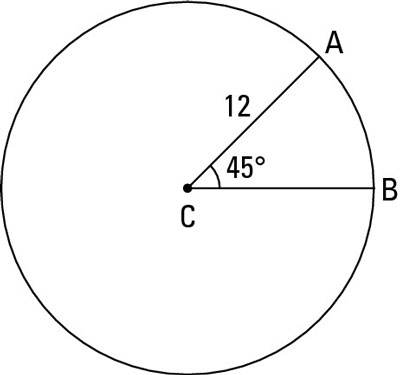
Arc length:

Its degree measure is 45° and the radius of the circle is 12, so here’s the math for its length:

Pretty simple, eh?






