Mark off a section of a circle with an arc and a chord, and you have a segment (this type of segment has nothing to do with a line segment). Throw a couple of radii around an arc, and you have a sector.
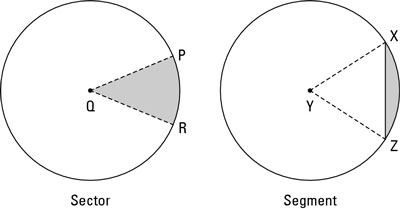
So here are the definitions of the two regions (The above figure shows you both):
*Sector: A region bounded by two radii and an arc of a circle (plain English definition: The shape of a piece of pizza)
*Segment of a circle: A region bounded by a chord and an arc of a circle
Area of a sector: The area of a sector (such as sector PQR in the above figure) is equal to the area of the circle
times the fraction of the circle represented by the sector:
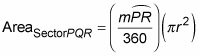
Here’s an example: using the following figure,
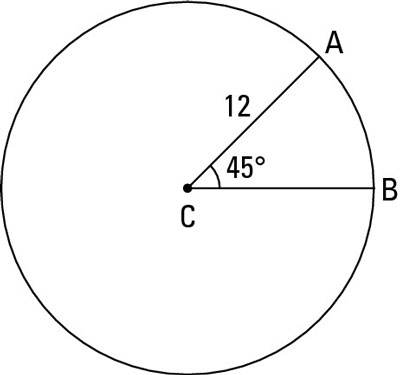
use the formula to find the area of sector ACB.

Area of a segment: To compute the area of a segment like the one in the first figure, just subtract the area of the triangle from the area of the sector (by the way, there’s no technical way to name segments, but you can call this one circle segment XZ):
The following problem illustrates how to find arc length, sector area, and segment area:

Here’s the solution:
Find the length of arc IK.
You really don’t need a formula for finding arc length if you understand the concepts:

That’s all there is to it. Here’s how all this looks when you plug it into the formula:

Find the area of sector IDK.
A sector is a fraction of the circle’s area. Because 120° takes up a third of the degrees in a circle, sector IDK occupies a third of the circle’s area. Here’s the formal solution:

Find the area of circle segment IK.
To find the segment area, you need the area of triangle IDK so you can subtract it from the area of sector IDK. Draw an altitude straight down from D to segment IK. That creates two 30°- 60°- 90° triangles.

You’re all set to finish with the segment area formula:






