There are different types of lines (or segments or rays) or pairs of lines (or segments or rays). You can identify single lines based on the direction they’re pointing (horizontal, vertical, or neither), and you can categorize pairs of lines based on whether they intersect or not, the angle they make with each other, and, whether they are coplanar or non-coplanar.
Defining horizontal and vertical lines
You probably already know what the terms horizontal and vertical mean, but here’s a refresher along with a handy-dandy figure.
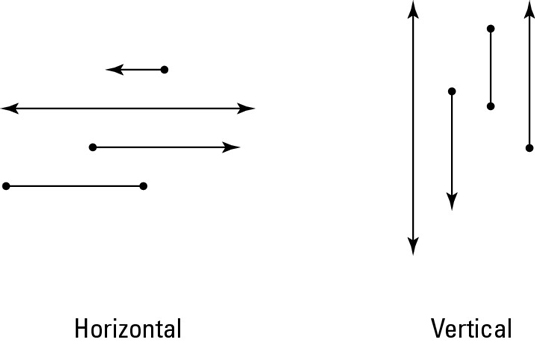
Horizontal lines, segments, or rays: Horizontal lines, segments, and rays go straight across, left and right, not up or down at all — you know, like the horizon.
Vertical lines, segments, or rays: Lines or parts of a line that go straight up and down are vertical. (Rocket science this is not.)
Defining pairs of lines
There are five terms that describe pairs of lines. The first four are about coplanar lines — you use these a lot. The fifth term describes non-coplanar lines. This term comes up only in 3-D problems.
Coplanar lines
Coplanar lines are lines in the same plane. Below are four terms that describe different ways coplanar lines may interact:
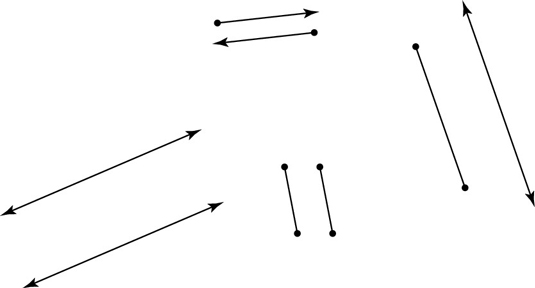
Parallel lines, segments, or rays: Lines that run in the same direction and never cross (like two railroad tracks) are called parallel. Segments and rays are parallel if the lines that contain them are parallel. See the above figure.
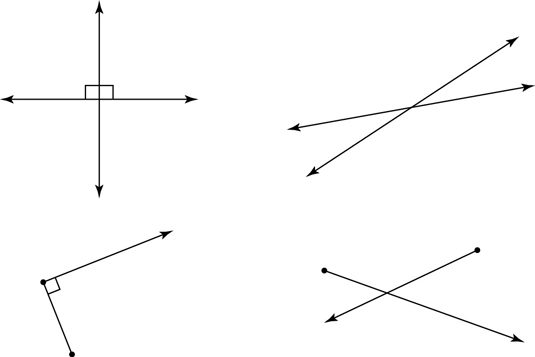
Intersecting lines, segments, or rays: Lines, segments, or rays that cross or touch are intersecting. The point where they cross or touch is called the point of intersection.
Perpendicular lines, segments, or rays: Lines, segments, or rays that intersect at right angles (90° angles) are perpendicular.
In the above figure, the little boxes in the corners of the angles indicate right angles.
Oblique lines, segments, or rays: Lines, segments, or rays that intersect at any angle other than 90° are called oblique. The above figure shows oblique lines and rays on the right.
Because lines extend forever, a pair of coplanar lines must be either parallel or intersecting. (However, this is not true for coplanar segments and rays. Segments and rays can be nonparallel and at the same time non-intersecting, because their endpoints allow them to stop short of crossing.)
Non-coplanar lines
Non-coplanar lines are simply lines that aren’t in the same plane.
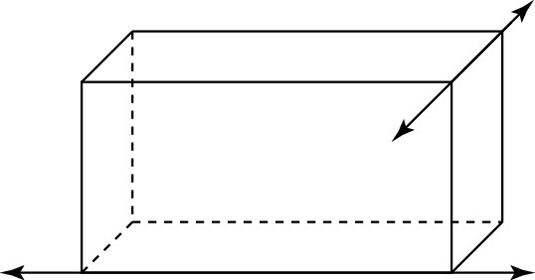
Skew lines, segments, or rays: Lines that don’t lie in the same plane are called skew lines — skew simply means non-coplanar. Or you can say that skew lines are lines that are neither parallel nor intersecting. The above figure shows an example. (You probably won’t ever hear anyone refer to skew segments or rays, but there’s no reason they can’t be skew. They’re skew if they’re non-coplanar.)
Here’s a good way to get a handle on skew lines. Take two pencils or pens, one in each hand. Hold them a few inches apart, both of them pointing away from you. Now, keep one where it is and point the other one up at the ceiling. That’s it. You’re holding skew lines.





