The way the midpoint formula works is very simple: It takes the average of the x-coordinates of the segment's endpoints and the average of the y-coordinates of the endpoints. These averages give you the location of a point that is exactly in the middle of the segment.
Midpoint formula: To find the midpoint of a segment with endpoints at (x1, y1) and (x2, y2), use the following formula:
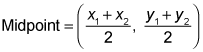
Note: It doesn't matter which point is (x1, y1) and which is (x2, y2).
Here's a problem that shows the midpoint formula in action.
Here is the proof diagram.
If you know your rectangle properties, you know that the diagonals of PQRS must bisect each other. But another way to show this is with coordinate geometry. The term bisect in this problem should ring the midpoint bell. So use the midpoint formula for each diagonal:
The fact that the two midpoints are the same shows that each diagonal goes through the midpoint of the other, and that, therefore, each diagonal bisects the other. Obviously, the diagonals cross at (6.5, 3). That's a wrap.








