Parallel lines are important when you study quadrilaterals because six of the seven types of quadrilaterals (all of them except the kite) contain parallel lines. The eight angles formed by parallel lines and a transversal are either congruent or supplementary.
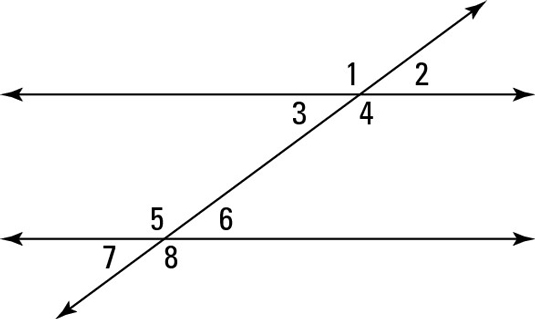
Check out the above figure which shows three lines that kind of resemble a giant not-equal sign. The two horizontal lines are parallel, and the third line that crosses them is called a transversal. As you can see, the three lines form eight angles.
The following theorems tell you how various pairs of angles relate to each other.
Proving that angles are congruent: If a transversal intersects two parallel lines, then the following angles are congruent (refer to the above figure):
Alternate interior angles: The pair of angles 3 and 6 (as well as 4 and 5) are alternate interior angles. These angle pairs are on opposite (alternate) sides of the transversal and are in between (in the interior of) the parallel lines.
Alternate exterior angles: Angles 1 and 8 (and angles 2 and 7) are called alternate exterior angles. They’re on opposite sides of the transversal, and they’re outside the parallel lines.
Corresponding angles: The pair of angles 1 and 5 (also 2 and 6, 3 and 7, and 4 and 8) are corresponding angles. Angles 1 and 5 are corresponding because each is in the same position (the upper left-hand corner) in its group of four angles.
Also notice that angles 1 and 4, 2 and 3, 5 and 8, and 6 and 7 are across from each other, forming vertical angles, which are also congruent.
Proving that angles are supplementary: If a transversal intersects two parallel lines, then the following angles are supplementary (see the above figure):
Same-side interior angles: Angles 3 and 5 (and 4 and 6) are on the same side of the transversal and are in the interior of the parallel lines, so they’re called (ready for a shock?) same-side interior angles.
Same-side exterior angles: Angles 1 and 7 (and 2 and 8) are called same-side exterior angles — they’re on the same side of the transversal, and they’re outside the parallel lines.
You can sum up the above definitions and theorems with the following simple, concise idea. When you have two parallel lines cut by a transversal, you get four acute angles and four obtuse angles (except when you get eight right angles). All the acute angles are congruent, all the obtuse angles are congruent, and each acute angle is supplementary to each obtuse angle. In short, any two of the eight angles are either congruent or supplementary.
Proving that lines are parallel: All these theorems work in reverse. You can use the following theorems to prove that lines are parallel. That is, two lines are parallel if they’re cut by a transversal such that
Two corresponding angles are congruent.
Two alternate interior angles are congruent.
Two alternate exterior angles are congruent.
Two same-side interior angles are supplementary.
Two same-side exterior angles are supplementary.





