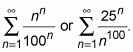The root test doesn’t compare a new series to a known benchmark series. It works by looking only at the nature of the series you’re trying to figure out. You use the root test to investigate the limit of the nth root of the nth term of your series. Like with the ratio test, if the limit is less than 1, the series converges; if it’s more than 1 (including infinity), the series diverges; and if the limit equals 1, you learn nothing.
The root test is a good one to try if the series involves nth powers.
Try this one: Does
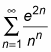
converge or diverge? Here’s what you do:
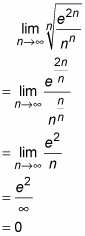
Because the limit is less than 1, the series converges.
Sometimes it’s useful to make an educated guess about the convergence or divergence of a series before you launch into one or more of the convergence/divergence tests. Here’s a tip that helps with some series. The following expressions are listed from “smallest” to “biggest”:
(The 10 is an arbitrary number; the size of the number doesn’t affect this ordering.) A series with a “smaller” expression over a “bigger” one converges, for example,
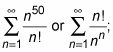
and a series with a “bigger” expression over a “smaller” one diverges, for instance,