For differentiating certain functions, logarithmic differentiation is a great shortcut. It spares you the headache of using the product rule or of multiplying the whole thing out and then differentiating. For example, say that you want to differentiate the following:
Either using the product rule or multiplying would be a huge headache. Instead, you do the following:
Take the natural log of both sides.
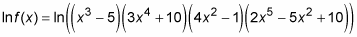
Now use the property for the log of a product.
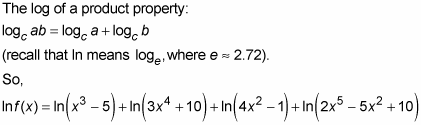
Differentiate both sides.

For each of the four terms on the right side of the equation, you use the chain rule.
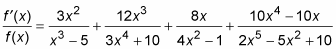
Multiply both sides by f (x), and you’re done.
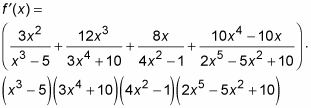
Granted, this answer is pretty hairy, and the solution process isn’t exactly a walk in the park, but this method is much easier than the other alternatives.

