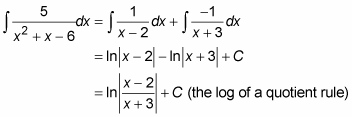You can use the partial fractions method to integrate rational functions (Recall that a rational function is one polynomial divided by another.) The basic idea behind the partial fraction approach is “unadding” a fraction:

Before using the partial fractions technique, you have to check that your integrand is a “proper” fraction — that’s one where the degree of the numerator is less than the degree of the denominator. If the integrand is “improper,” like
you have to first do long polynomial division to transform the improper fraction into a sum of a polynomial (which sometimes will just be a number) and a proper fraction. Here’s the division for this improper fraction (without explanation). Basically, it works just like regular long division.
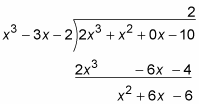
With regular division, if you divide 4 into 23, you get a quotient of 5 and a remainder of 3, which tells you that
The result of the above polynomial division tells you the same thing.

The first integral is just 2x. You would then do the second integral with the partial fractions method.
Here’s how the method works, but let’s tackle a less complicated integral than the one immediately above; this will make the technique easier to follow.
Factor the denominator.
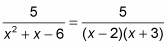
Break up the fraction on the right into a sum of fractions, where each factor of the denominator in Step 1 becomes the denominator of a separate fraction. Then put unknowns in the numerator of each fraction.
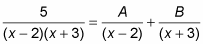
Multiply both sides of this equation by the denominator of the left side.
This is algebra I, so you can’t possibly want to see the steps. Right?
5 = A(x + 3) + B(x – 2)
Take the roots of the linear factors and plug them — one at a time — into x in the equation from Step 3, and solve for the unknowns.
If x = 2
5 = A(2 + 3) + B(2 – 2)
5 = 5A
A = 1
Or if x = –3
5 = A(–3 + 3) + B(–3 – 2)
5 = –5B
B = –1
Plug these results into the A and B in the equation from Step 2.
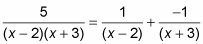
Split up the original integral into the partial fractions from Step 5 and you’re home free.