Geometry tells you how to figure the volumes of simple solids. Integration enables you to calculate the volumes of an endless variety of much more complicated shapes. If you have a circular shape with a circular hole in the center, you can use the washer method to find its volume by cutting the shape into thin pieces and then adding up the volumes of the slices. There’s nothing to it.
Here you go.
and generate a solid by revolving that area about the x-axis.
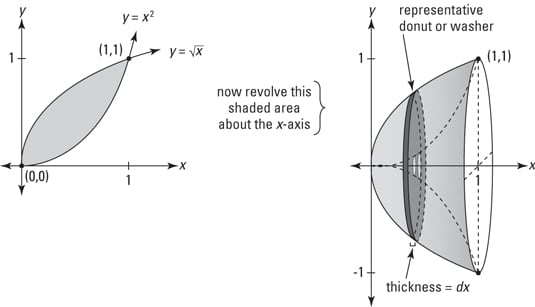
Just think: All the forces of the evolving universe and all the twists and turns of your life have brought you to this moment when you are finally able to calculate the volume of this weird bowl-like shape — something for your diary. So what’s the volume?
Determine where the two curves intersect.

So the solid in question spans the interval on the x-axis from 0 to 1.
Figure the area of a cross-sectional washer.
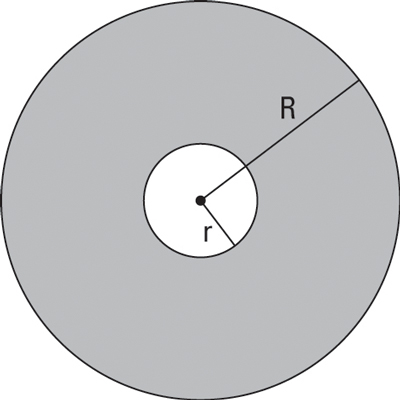
The figure immediately above shows a typical cross section of the 3-D shape, but turned so you’re looking at it head on. Each slice has this washer shape so its area equals the area of the entire circle minus the area of the hole.
The area of the circle minus the hole is
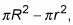
where R is the outer radius (the big radius) and r is the radius of the hole (the little radius).
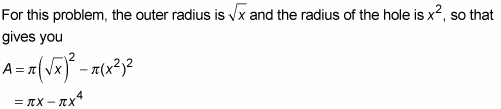
Multiply this area by the thickness, dx, to get the volume of a representative washer.
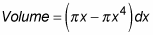
Add up the volumes of the washers from 0 to 1 by integrating.
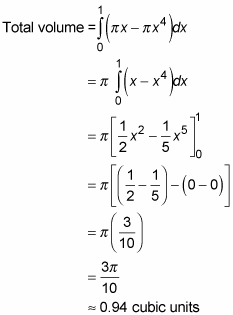
Focus on the simple fact that the area of a washer is the area of the entire disk,
minus the area of the hole,
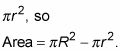
When you integrate, you get
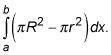
This is the same, of course, as
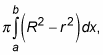
which is the formula given in most books. But if you just learn that by rote, you may forget it. You’re more likely to remember how to do these problems if you understand the simple big-circle-minus-little-circle idea.

