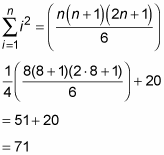How to Do an Area Approximation Using Sigma Notation

Sigma notation comes in handy when you’re approximating the area under a curve. For example, express an 8-right-rectangle approximation of the area under

from 0 to 4 and compute the approximation.

1. Express the basic idea of your sum:

   

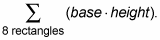
This just means that you’re adding up the areas of 8 rectangles, each of which has an area of base times height.

1. Figure the base and plug in.

   

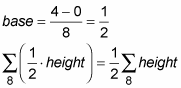
Constants, like 1/2, can be pulled through the sigma symbol.

1. Add the limits of summation, and express the height as a function of the index of summation:

Since each rectangle has a base of 1/2, the right edge of the first rectangle will be at 1/2; the right edge of the second rectangle will be at 2/2, or 1; the right edge of the third will be at 3/2, etc. That’s what the does above. If you plug 1 then 2 then 3, etc. up to 8 into i, you get the locations of the right edges of all 8 rectangles.

1. Plug in your function,

   

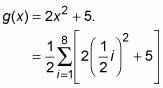
2. Simplify:

   

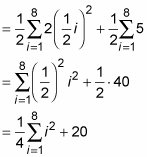
3. Use the sum of squares rule to finish: