You can add up minute lengths along a curve, an arc, to get the whole length. When you analyze arc length, you divide a length of curve into small sections, figure the length of each section, and then add up all the lengths. The following figure shows how each section of a curve can be approximated by the hypotenuse of a tiny right triangle.
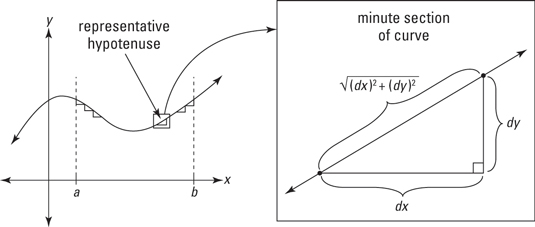
You can imagine that as you zoom in further and further, dividing the curve into more and more sections, the minute sections get straighter and straighter and the hypotenuses better and better approximate the curve. That’s why — when this process of adding up smaller and smaller sections is taken to the limit — you get the precise length of the curve.
So, all you have to do is add up all the hypotenuses along the curve between your start and finish points. The lengths of the legs of each infinitesimal triangle are dx and dy, and thus the length of the hypotenuse — given by the Pythagorean Theorem — is
To add up all the hypotenuses from a to b along the curve, you just integrate:
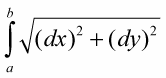
A little tweaking and you have the formula for arc length.

The arc length along a curve, y = f(x), from a to b, is given by the following integral:
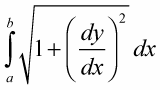
The expression inside this integral is simply the length of a representative hypotenuse.
Try this one: What’s the length along
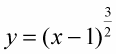
from x = 1 to x = 5?
Take the derivative of your function.
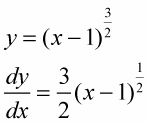
Plug this into the formula and integrate.
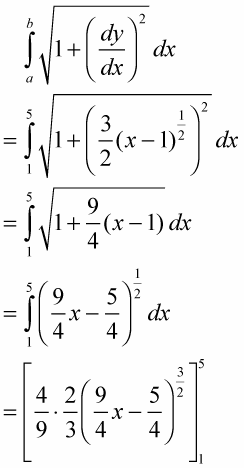
(See how this works? It’s the guess-and-check integration technique with the reverse power rule. The 4/9 is the tweak amount you need because of the coefficient 9/4.)

Now, if you ever find yourself on a road with the shape of
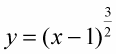
and your odometer’s broken, you can figure the exact length of your drive. Your friends will be very impressed — or very concerned.

