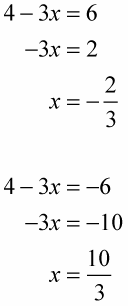A linear absolute value equation is an equation that takes the form |ax + b| = c. Taking the equation at face value, you don’t know if you should change what’s in between the absolute value bars to its opposite, because you don’t know if the expression is positive or negative. The sign of the expression inside the absolute value bars all depends on the sign of the variable x. To solve an absolute value equation in this linear form, you have to consider both possibilities: ax + b may be positive, or it may be negative.
To solve for the variable x in |ax + b| = c, you solve both ax + b = c and ax + b = –c.
For example, to solve the absolute value equation |4x + 5| = 13, you write the two linear equations and solve each for x:
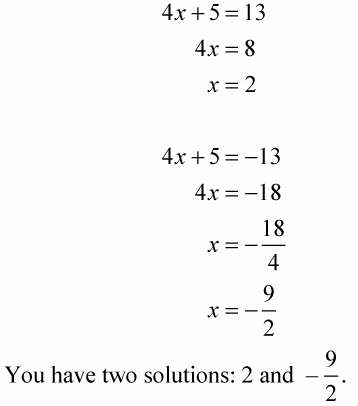
Both solutions work when you replace the x in the original equation with their values.
One restriction you should be aware of when applying the rule for changing from absolute value to individual linear equations is that the absolute value term has to be alone on one side of the equation.
For instance, to solve 3|4 – 3x| + 7 = 25, you have to subtract 7 from each side of the equation and then divide each side by 3:
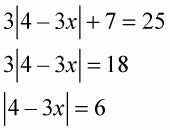
Now you can write the two linear equations and solve them for x: