Distribution problems with fractional powers or radicals aren't as intimidating as they look. When distributing with fractional powers or radicals, remember that exponents that are fractions work the same way as exponents that are integers — they’re added together. The only hitch is that the fractions have to have the same denominator to be added. With radicals, you just change them to expressions with fractions as exponents.
Try the following distribution problem with exponents that are fractions to get an idea of how to work through it.
Example:
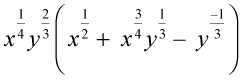
Distribute the following:

Here's how.

Rearrange the variables and add exponents.

Add the fractions.

Distribution is easier in this case if you first change everything to fractional exponents. Radicals can be changed to expressions with fractions as exponents by making the root of the radical the denominator of the fractional exponent, as in the following examples:
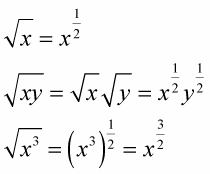
The exponent rule for raising a product within parentheses to a power is to multiply each power in the parentheses by the outside power. For example,
Change the radical notation to fractional exponents.

Raise the powers.

Distribute the outside term over each term within the parentheses.

Add the exponents of the variables.

Simplify the fractions.






