Graphically, the solution is the point or points where the lines or curves intersect. This means to solve a system of equations (linear, quadratic, and so on) by graphing, you follow these steps:
- Graph each function independently but on the same coordinate plane.
- Look for the point or points where the functions intersect.
- Test the points you identified by substituting them into all original equations. While this step is optional, it's highly recommended because graphs can be drawn inaccurately if generated by hand.
Practice question
- Which system of equations is represented by the following graph?
A. y = 2x – 1; y = x + 3 B. y = –2x + 3; y = x – 1 C. y = –x + 3; y = 2x – 1 D. y = –x –1; y = 2x + 3
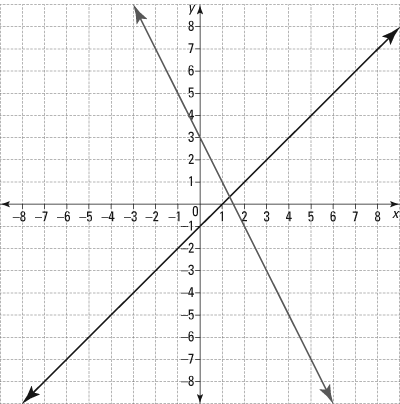
Answer and explanation
- The correct answer is Choice (B). The first thing to do is identify the y-intercepts: 3 and –1. Now find the slopes of the lines associated with each of the y-intercepts; the line with a y-intercept of 3 has a negative slope, which eliminates Choices (A) and (C). Further inspection allows you to conclude that the slope associated with 3 is –2, while the slope of the line with the y-intercept of –1 is 1. This means the equation of the two lines is y = –2x + 3 and y = x – 1, which is Choice (B).

