To save time when graphing a quadratic function on the ACT Math test, you can quickly find the location of the y-intersept of the parabola based on the sign of the variable c.
The variable c is the constant term of the quadratic equation, y = ax2 + bx + c.
Keep the following rules in mind:
When c is positive, the y-intercept is positive. In other words, the parabola intersects the y-axis above the origin.
When c is negative, the y-intercept is negative. That is, the parabola intersects the y-axis below the origin.
Warning: Be clear that in a quadratic function, c is the y-intercept. In contrast, in a linear function
b is the y-intercept.
Example
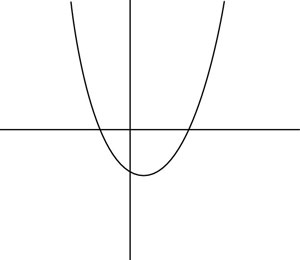
Which of the following could be a graph of the function y = –x2 + 5x – 2?
(A)
(B)
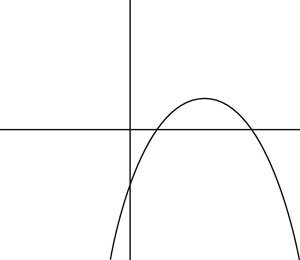
(C)
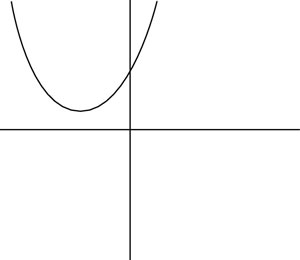
(D)
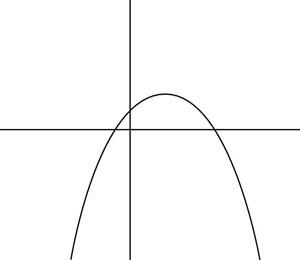
(E)
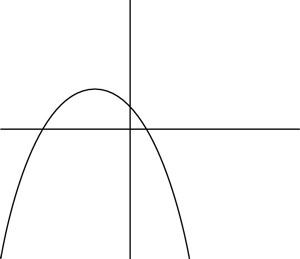
In this equation, c = –2, so the y-intercept is below the y-axis. As a result, you can rule out Choices (C), (D), and (E). Additionally, a = –1, so the parabola is concave down. So you also can rule out Choice (A), which makes the correct answer Choice (B).

