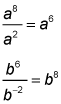ACT Practice Math Questions: Exponents

Practice questions

1. If
   
   what is the value of c? A. 2 B. 4 C. 8 D. 16 E. 32
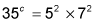
2. For all
   
   A. 8a⁶b⁸ B. 8a⁶b⁴ C. 8a⁴b⁷ D. 2a⁶b⁸ E. 2a⁴b⁷

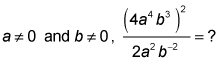
Answers and explanations

1. The correct answer is Choice (A). You can answer this question super quickly when you recognize that when you multiply numbers with the same exponents, the exponents stay the same. That means in this multiplication problem all of the exponents on either side of the equation must have the same value:
   
   Because the value of the exponents on the right side of the equation is 2, c must be 2. You can also figure the answer by simplifying the right side of the equation and then play with your calculator to find out what power of 35 that is. The right side of the equation simplifies as follows:
   
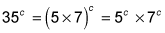   So 35^c = 1,225. Turns out 1,225 is 35 times 35 or 35². c still equals 2.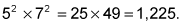
2. The correct answer is Choice (A). This question requires basic simplification. Begin by canceling terms. Because the whole numerator is squared, you first need to square every term in the parentheses. 4² = 16 Divide the coefficients of 16 and 2 to get 8; eliminate Choices (D) and (E) because they don't have a coefficient of 8. Continue by squaring the variables in the numerator. When you take an exponent to another power, you multiply the exponents:
   
   The new expression is
   
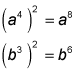   Divide the variables by subtracting the exponents:
   
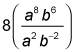   Combine the components to get a final answer of 8a⁶b⁸. If you picked Choice (B), you subtracted the 2 from 6 when you worked with the b exponents. When you subtract a negative value, you actually add the value. If you picked Choice (C), you added the exponents when you squared them instead of multiplying them.