In a binary heap, the root node always contains the smallest value. When viewing the branches, you see that upper-level branches are always a smaller value than lower-level branches and leaves. The effect is to keep the tree balanced and in a predictable order so that searching becomes extremely efficient. The cost is in keeping the tree balanced.
Of all the tasks that applications do, searching is the more time consuming and also the one required most. Even though adding data (and sorting it later) does require some amount of time, the benefit to creating and maintaining a dataset comes from using it to perform useful work, which means searching it for important information. Consequently, you can sometimes get by with less efficient CRUD functionality and even a less-than-optimal sort routine, but searches must proceed as efficiently as possible. The only problem is that no one search performs every task with absolute efficiency, so you must weigh your options based on what you expect to do as part of the search routines.
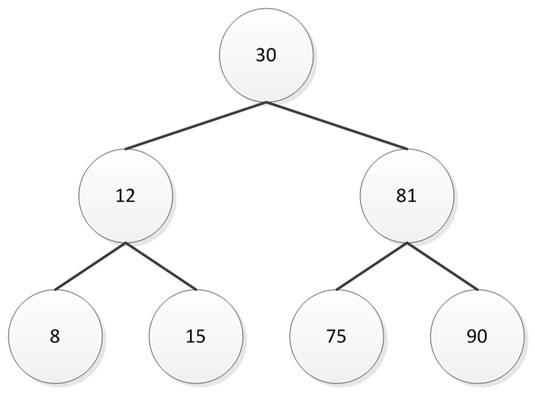
Two of the more efficient methods of searching involve the use of the binary search tree (BST) and binary heap. Both of the search techniques rely on a tree-like structure to hold the keys used to access data elements. However, the arrangement of the two methods is different, which is why one has advantages over the other when performing certain tasks. This figure shows the arrangement for a BST.
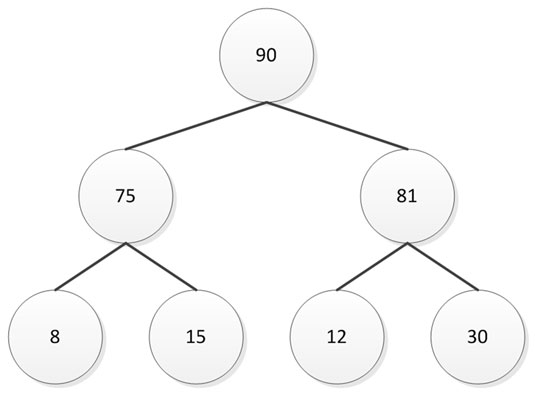
Note how the keys follow an order in which lesser numbers appear to the left and greater numbers appear to the right. The root node contains a value that is in the middle of the range of keys, giving the BST an easily understood balanced approach to storing the keys. Contrast this arrangement to the binary heap shown here.
Each level contains values that are less than the previous level, and the root contains the maximum key value for the tree. In addition, in this particular case, the lesser values appear on the left and the greater on the right (although this order isn't strictly enforced). The figure actually depicts a binary max heap. You can also create a binary min heap in which the root contains the lowest key value and each level builds to higher values, with the highest values appearing as part of the leaves.
As previously noted, BST has some advantages over binary heap when used to perform a search. The following list provides some of the highlights of these advantages:
- Searching for an element requires O(log n) time, contrasted to O(n) time for a binary heap.
- Printing the elements in order requires only O(log n) time, contrasted to O(n log n) time for a binary heap.
- Finding the floor and ceiling requires O(log n) time.
- Locating Kth smallest/largest element requires O(log n) time when the tree is properly configured.
- Creating the required structures requires fewer resources because binary heaps rely on arrays, making them cache friendlier as well.
- Building a binary heap requires O(n) time, contrasted to BST, which requires O(n log n) time.
- Using pointers to implement the tree isn't necessary.
- Relying on binary heap variations (for example, the Fibonacci Heap) offers advantages such as increase and decrease key times of O(1) time.