The z-transform (ZT) is a generalization of the discrete-time Fourier transform (DTFT) for discrete-time signals, but the ZT applies to a broader class of signals than the DTFT. The two-sided or bilateral z-transform (ZT) of sequence x[n] is defined as
The ZT operator transforms the sequence x[n] to X(z), a function of the continuous complex variable z. The relationship between a sequence and its transform is denoted as
You can establish the connection between the discrete-time Fourier transform (DTFT) and the ZT by first writing
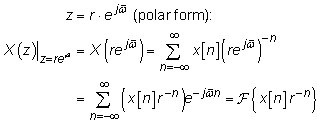
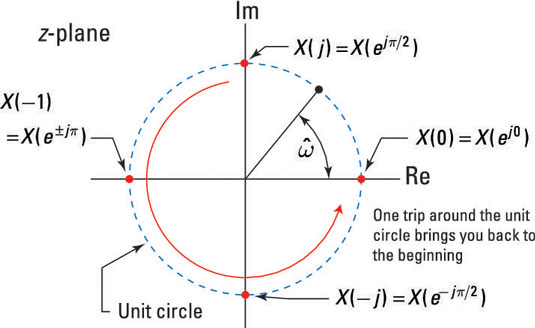
The special case of r = 1 evaluates X(z) over the unit circle —
and is represented as
the DTFT of x[n]. This result holds as long as the DTFT is absolutely summable (read: impulse functions not allowed).
The view that
sampled around the unit circle in the z-plane
shows that the DTFT has period 2π because