A type of signal classification you need to be able to determine is periodic versus aperiodic. A signal is periodic if x(t) = x(t + T0), where T0, the period, is the largest value satisfying the equality. If a signal isn’t periodic, it’s aperiodic.
When checking for periodicity, you’re checking in a graphical sense to see whether you can copy a period from the center of the waveform, shift it left or right by an integer multiple of T0, and if it perfectly matches the signal T0 seconds away. The single sinusoid signal is always periodic, and the proof, which relies on simple trigonometry, allows you to determine what the period is.
To establish that a single sinusoid signal is periodic and to determine the period, follow these steps:
Ask yourself: What does it take to make the equality hold?
Making the arguments equal seems to be the only option.
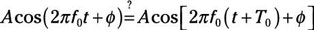
Expand the argument of the cosine on the right side to see the impact of the added T0:
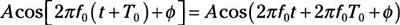
Cosine is a modulo 2π function; that is, the functional values it produces don’t change when the argument is shifted by integer multiples of 2π, which makes the single sinusoid a periodic signal from the get-go.
To establish the period, observe that forcing
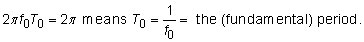
Because T0 is the fundamental period, f0 is the fundamental frequency; they’re reciprocals.
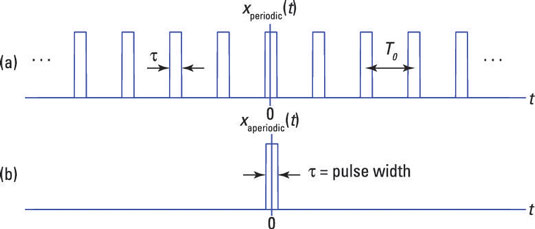
Part (a) of the following figure shows a periodic signal known as a periodic pulse train because it has an infinite train of pulses. Each pulse has width
and the ellipsis indicate that the pulse train continues in both directions. The pulses that follow each other don’t have to be periodic, though. In part (b), a waveform with a single isolated pulse or just a few pulses makes the signal aperiodic.