With the simplification to the open-loop system function in place, you can dive in and find the closed-loop system function of the CD/DVD case study, with full variable substitution. Here’s the closed-loop system function H(s) with the simplified open-loop system function applied:
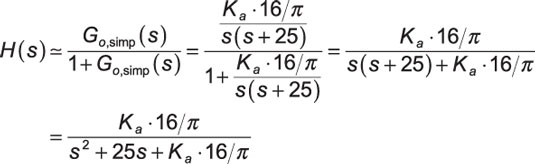
With Ka = 50, you have a natural frequency of 15.95 rad/s and damping factor of 0.78.
The feedback connection has definitely changed things. There’s no longer a pole at s = 0. The roots given Ka = 50 are
In [<b>83</b>]: Ka = 50 In [<b>84</b>]: roots([1, 25, Ka*16/pi]) Out[<b>84</b>]: array([-12.5+9.91957201j, -12.5-9.91957201j])
This is a complex conjugate pole pair in the left-half plane, so H(s) is stable! Check the exact G0(s) model. After working through the math by hand to find H(s), you can use PyLab to numerically root the denominator polynomial:
In [<b>85</b>]: roots([1, 1250+25, 25*1250, Ka*4000*10/(2*pi)]) Out[<b>85</b>]: array([-1250.21 +0.j, -12.396+10.047j, -12.396-10.047j])
The complex conjugate root pair for the exact closed-loop model is close to the simplified model. A third real root is included at –1,250 rad/s, again resulting in a time constant that decays very rapidly relative to the complex conjugate poles.
The frequency response, magnitude, and phase plots also play a role in control system design. To plot the frequency response, use w,H=freqs(b,a,w) from the signal package:
In [<b>145</b>]: w = logspace(0,4,500) In [<b>146</b>]: b,a = ssd.position_CD(50,'fb_approx') In [<b>147</b>]: w,H_simple = signal.freqs(b,a,w) In [<b>148</b>]: b,a = ssd.position_CD(50,'fb_exact') In [<b>149</b>]: w,H_exact = signal.freqs(b,a,w) In [<b>151</b>]: semilogx(w,20*log10(abs(H_simple))) In [<b>152</b>]: semilogx(w,20*log10(abs(H_exact)),'r') In [<b>156</b>]: semilogx(w,angle(H_simple)*180/pi) In [<b>157</b>]: semilogx(w,angle(H_exact)*180/pi,'r')
![[Credit: Illustration by Mark Wickert, PhD]](https://www.dummies.com/wp-content/uploads/379650.image1.jpg)
The third pole at 1,250 rad/s (from the exact model) kicks in at about 80 dB of loop attenuation. This has little impact on the closed-loop performance as long as the loop gain isn’t too large.

