When you place a book on a table, it doesn’t accelerate down toward Earth, even though Earth’s gravity is pulling the book down, because a second force, from the table, is pushing up on the book and balancing the force from gravity. The book is in equilibrium. An object is in equilibrium if all the forces on it exactly cancel out.
Sample question
The figure shows three connected ropes. If rope A has a tension of 10 N at 135 degrees and rope B has a tension of 10 N at 45 degrees, what must the tension in rope C be to keep things in equilibrium?
The correct answer is 14 N downward.
Convert tension A into vector component notation. Use the equation Ax = A cos theta to find the x coordinate of the tension from rope A: 10.0 cos 135 degrees = –7.07 N.
Use the equation Ay = A sin theta to find the y coordinate of the tension from rope A: 10.0 sin 135 degrees, or 7.07 N. That makes the tension A (–7.07, 7.07)N in coordinate form.
Convert the tension B into components. Use the equation Bx = B cos theta to find the x coordinate of the tension from rope B: 10.0 cos 45 degrees = 7.07 N.
Use the equation By = B sin theta to find the y coordinate of the second tension: 10.0 sin 45 degrees, or 7.07 N. That makes the tension B (7.07, 7.07)N in coordinate form.
5.Perform vector addition to find the net tension: (–7.07, 7.07)N + (7.07, 7.07)N = (0, 14.1)N.
To counteract the total tension from ropes A and B, the tension in rope C must be 14.1 N downward (that is, –14.1 N). With significant figures, this answer rounds to 14 N downward.
Practice questions
You have three ropes tied together in equilibrium. The tension in rope A is 15 N at 135 degrees, and the tension in rope B is 15 N at 45 degrees. What must the tension in rope C be?
You have three ropes tied together in equilibrium. The tension in rope A is 17.0 N at 115 degrees, and the tension in rope B is 18.0 N at 25 degrees. What must the tension in rope C be?
Following are answers to the practice questions:
21 N downward
Convert tension A into vector component notation. Use the equation Ax = A cos theta to find the x coordinate of tension A: 15.0 cos 135 degrees = –10.6 N.
Use the equation Ay = A sin theta to find the y coordinate of tension A: 15.0 sin 135 degrees = 10.6. That makes tension A (–10.6, 10.6)N in coordinate form.
Convert tension B into components. Use the equation Bx = B cos theta to find the x coordinate of tension B: 15.0 cos 45 degrees = 10.6 N.
Use the equation By = B sin theta to find the y coordinate of tension B: 15.0 sin 45 degrees = 10.6 N. That makes tension B (10.6, 10.6)N in coordinate form.
Perform vector addition to find the net tension: (–10.6, 10.6)N + (10.6, 10.6)N = (0, 21.2)N.
To counteract this tension, the tension in rope C must have a magnitude of 21.2 N and point downward. With significant figures, the magnitude is rounded to 21 N.
24.7 N at 248 degrees
Convert tension A into vector component notation. Use the equation Ax = A cos theta to find the x coordinate of tension A: 17.0 cos 115 degrees = –7.18 N.
Use the equation Ay = A sin theta to find the y coordinate of tension A: 17.0 sin 115 degrees = 15.4. That makes tension A (–7.18, 15.4)N in coordinate form.
Convert tension B into components. Use the equation Bx = B cos theta to find the x coordinate of tension B: 18.0 cos 25 degrees = 16.3 N.
Use the equation By = B sin theta to find the y coordinate of tension B: 18.0 sin 25 degrees = 7.61. That makes tension B (16.3, 7.61)N in coordinate form.
Perform vector addition to find the net tension: (–7.18, 15.4)N + (16.3, 7.61)N = (9.1, 23.0)N.
Find the angle of the tension due to A and B: theta= tan–1(y/x) = tan–1(2.53) = 68 degrees.
Apply the equation
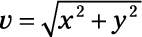
to find the magnitude of tension due to A and B, giving you 24.7 N.
Find the angle of the tension in rope C. This must be opposite the tension due to A and B, which is 68 degrees + 180 degrees = 248 degrees.

