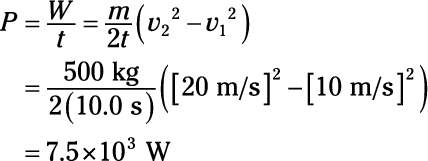When it comes to work in physics, you’re sure to see problems involving power, which is the amount of work being done in a certain amount of time. Here’s the equation for power, P:
W equals force along the direction of travel times distance, so you could write the equation for power this way:
where theta is the angle between the force and the direction of travel. On the other hand, the object’s speed, v, is just s/t (displacement over time), so the equation breaks down further to:
In the special case where the force acts along the direction of travel, you have the simplified formula:
So in this simplest case, power equals force times speed. You use this equation when you need to apply a force to keep something moving at constant speed.
Sample question
You’re riding a toboggan down an icy run to a frozen lake, and you accelerate the 80.0-kg combination of you and the toboggan from 1.0 m/s to 2.0 m/s in 2.0 s. How much power does that require?
The correct answer is 60 watts.
Assuming that there’s no friction on the ice, you use this equation for the total work:
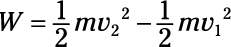
Plug in the numbers:
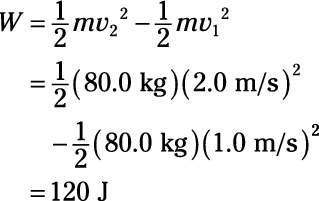
Because this work is done in 2 s, the power involved is

Practice questions
1.A 1,000-kg car accelerates from 88 m/s to 100 m/s in 30 s. How much power does that require?
A 60.0-kg person is running and accelerates from 5.0 m/s to 7.0 m/s in 2.0 s. How much power does that require?
3.A 120-kg linebacker accelerates from 5.0 m/s to 10.0 m/s in 1.0 s. How much power does that require?
4.You’re driving a snowmobile that accelerates from 10 m/s to 20 m/s over a time interval of 10.0 s. If you and the snowmobile together have a mass of 500 kg, how much power is used?
Following are answers to the practice questions:
3.8 x 104 watts
The equation for power is
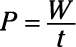
The amount of work done is the difference in kinetic energy:
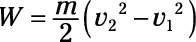
Therefore, the power is
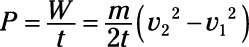
Plug in the numbers:
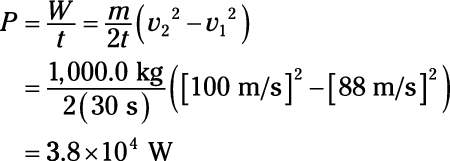
360 W
The equation for power is
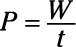
The amount of work done is the difference in kinetic energy:
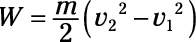
Therefore, the power is
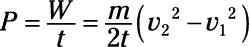
Plug in the numbers:
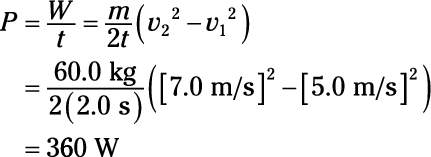
4,500 W
The equation for power is
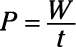
The amount of work done is the difference in kinetic energy:
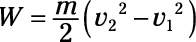
Therefore, the power is
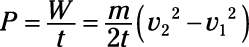
Plug in the numbers:
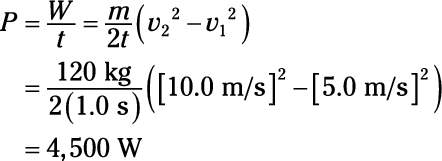
7.5 x 103 W
The equation for power is

The amount of work done is the difference in kinetic energy:
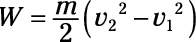
Therefore, the power is
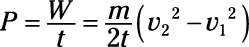
Plug in the numbers: