Newton says sigmaF = ma, which means that you add all the force vectors together to get the net force. That’s how it usually works when you have to figure out F = ma problems in physics. Often, a number of force vectors are involved, and you have to solve for the net force to find the acceleration.
Take a look at the hockey puck in the figure. Two forces, A and B, are acting on the puck. What’s going to happen to the puck?
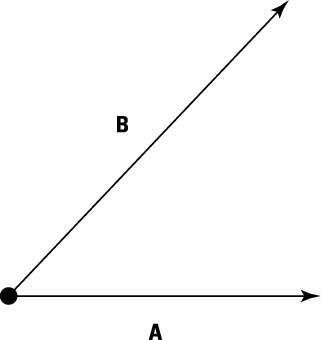
You don’t have to calculate the result of each force acting separately on the hockey puck because the net force is what’s important. Calculate the net force first and then use that in sigmaF = ma.
Sample question
Suppose that the forces acting on the hockey puck are A = 9.0 N at 0 degree, and B = 14.0 N at 45 degrees. What is the acceleration of the puck, given that its mass is 1.00 x 10–1 kg?
The correct answer is magnitude 213 m/s2, angle 28 degrees.
Convert force A into vector component notation. Use the equation Ax = A cos theta to find the x coordinate of the force: 9.0 cos 0 degree = 9.0.
Use the equation Ay = A sin theta to find the y coordinate of the force: 9.0 sin 0 degree, or 0.0. That makes the vector A (9.0, 0.0) in coordinate form.
Convert the vector B into components. Use the equation Bx = B cos theta to find the x coordinate of the acceleration: 14.0 cos 45 degrees = 9.9.
Use the equation By = B sin theta to find the y coordinate of the second force: 14.0 sin 45 degrees, or 9.9. That makes the force B (9.9, 9.9) in coordinate form.
5.Perform the vector addition to find the net force: (9.0, 0.0) + (9.9, 9.9) = (18.9, 9.9).
Convert the vector (18.9, 9.9) into magnitude/angle form. Use the equation theta = tan–1(y/x) to find the angle of the net force: tan–1(0.52) = 28 degrees.
Apply the equation
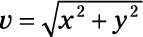
to find the magnitude of the net force, giving you 21.3 N.
Convert 21.3 N into acceleration: a = F/m = (21.3 N)/(0.100 kg) = 213 m/s2.
Practice questions
Assume that the two forces acting on a 0.10-kg hockey puck are as follows: A is 16.0 N at 53 degrees, and B is 21.0 N at 19 degrees. What is the acceleration of the hockey puck?
Two forces act on a 1.0 x 103 kg car. A is 220 N at 64 degrees, and B is 90.0 N at 80 degrees. What is the car’s acceleration?
3.Suppose that two forces act on a 100-kg boat. A is 100 N at 10 degrees, and B is 190 N at 210 degrees. What is the boat’s acceleration?
A marble with a mass of 1.0 g is hit by two other marbles that each apply a force for 0.3 seconds. If force A is 0.010 N at 63 degrees and B is 0.050 N at 135 degrees, what is the acceleration of the original marble?
Following are answers to the practice questions:
Magnitude: 354 m/s2; Angle: 34 degrees
Convert force A into its components. Use the equation Ax = A cos theta to find the x coordinate of force A: 16.0 cos 53 degrees = 9.6 N.
Use the equation Ay = A sin theta to find the y coordinate of force A: 16.0 sin 53 degrees = 12.8. That makes force A (9.6, 12.8)N in coordinate form.
Convert force B into its components. Use the equation Bx = B cos theta to find the x coordinate of force B: 21.0 cos 19 degrees = 19.9 N.
Use the equation By = B sin theta to find the y coordinate of force B: 21.0 sin 19 degrees = 6.8. That makes force B (19.9, 6.8)N in coordinate form.
Perform vector addition to find the net force: (9.6, 12.8)N + (19.9, 6.8)N = (29.5, 19.6)N.
Convert the vector (29.5, 19.6)N into magnitude/angle form. Use the equation theta = tan–1(y/x) to find the angle of the net force: tan–1(0.66) = 34 degrees. The direction of the acceleration is the same as the direction of the net force: 34 degrees.
Apply the equation
to find the magnitude of the net force, giving you 35.4 N. Use the magnitude of the force and the mass to find the magnitude of the acceleration: a = F/m = (35.4 N)/(0.10 kg) = 354 m/s2.
Magnitude: 0.31 m/s2; Angle: 69 degrees
Convert force A into its components. Use the equation Ax = A cos theta to find the x coordinate of force A: 220 cos 64 degrees = 96 N.
Use the equation Ay = A sin theta to find the y coordinate of the force: 220 sin 64 degrees = 198 N. That makes force A (96, 198)N in coordinate form.
Convert force B into its components. Use the equation Bx = B cos theta to find the x coordinate of force B: 90 cos 80 degrees = 16 N.
Use the equation By = B sin theta to find the y coordinate of force B: 90 sin 80 degrees = 89 N. That makes force B (16, 89)N in coordinate form.
Perform vector addition to find the net force: (96, 198)N + (16, 89)N = (112, 287)N.
Convert the vector (112, 287)N into magnitude/angle form. Use the equation theta = tan–1(y/x) to find the angle of the net force: tan–1 (2.56) = 69 degrees. The direction of the acceleration is the same as the direction of the net force: 69 degrees.
Apply the equation
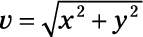
to find the magnitude of the net force, giving you 308 N.
Use the magnitude of the force and the mass to find the magnitude of the acceleration: a = F/m = (308 N)/(1,000 kg) = 0.31 m/s2.
Magnitude: 1 m/s2; Angle: 229 degrees
Convert force A into its components. Use the equation Ax = A cos theta to find the x coordinate of force A: 100 cos 10 degrees = 98 N.
Use the equation Ay = A sin theta to find the y coordinate of force A: 100 sin 10 degrees = 17. That makes force A (98, 17)N in coordinate form.
Convert force B into its components. Use the equation Bx = B cos theta to find the x coordinate of force B: 190 cos 210 degrees = –165 N.
Use the equation By = B sin theta to find the y coordinate of force B: 190 sin 210 degrees = –95. That makes force B (–165, –95)N in coordinate form.
Perform vector addition to find the net force: (98, 17)N + (–165, –95)N = (–67, –78)N.
Convert the vector (–67, –78)N into magnitude/angle form. Use the equation theta = tan–1(y/x) to find the angle of the net force: tan–1(1.2) = 49 degrees. But that answer’s not right because both components are negative, which means that the angle is actually between 180 degrees and 270 degrees. Add 180 degrees to 49 degrees to get 229 degrees. The acceleration is in the same direction as the net force.
Apply the equation
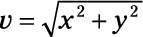
to find the magnitude of the net force, giving you 102 N.
Use the magnitude of the force and the mass to find the magnitude of the acceleration: a = F/m = (102 N)/(100 kg) = 1.0 m/s2.
Magnitude: 54 m/s2; Angle: 125 degrees
Convert force A into its components. Use the equation Ax = A cos theta to find the x coordinate of force A: 0.01 cos 63 degrees = 4.5 x 10–3N.
Use the equation Ay = A sin theta to find the y coordinate of force A: 0.01 sin 63 degrees = 8.9 x 10–3N. That makes force A (4.5 x 10–3, 8.9 x 10–3)N in coordinate form.
Convert force B into its components. Use the Bx = B cos theta to find the x coordinate of force B: 0.05 cos 135 degrees = –3.5 x 10–2N.
Use the equation By = B sin theta to find the y coordinate of force B: 0.05 sin 135 degrees = 3.5 x 10–2N. That makes force B (–3.5 x 10–2, 3.5 x 10–2)N in coordinate form.
Perform vector addition to find the net force: (4.5 x 10–3, 8.9 x 10–3)N + (–3.5 x 10–2, 3.5 x 10–2)N = (–3.1 x 10–2, 4.4 x 10–2)N.
Convert the vector (–3.1 x 10–2, 4.4 x 10–2)N into magnitude/angle form. Use the equation theta = tan–1(y/x) to find the angle of the net force: tan–1(1.42) = 125 degrees. The acceleration is in the same direction as the net force.
Apply the equation
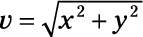
to find the magnitude of the net force, giving you 5.4 x 10–2 N.
Use the magnitude of the force and the mass to find the magnitude of the acceleration: a = F/m = 5.4 x 10–2/0.001 = 54 m/s2.

