The following list discusses the most common errors people make when working out physics problems. For those who teach physics, certain types of problems stand out, and you see them here.
Mixing units
The most common error made in solving physics problems involves mixing the units from one system with another system. If the problem is given to you in inches, kilograms, and seconds, convert it into a consistent system of units before proceeding to work out the answer. The most common system of units in physics is the meters-kilograms-seconds or MKS system. Newtons, watts, and volts are all units in this system. If you want to use the MKS system, convert everything into MKS before working out the problem.
Expressing the answer in the wrong units
If the problem asks for the answer in the MKS system, don't give it in CGS units. You'd be surprised at how common an error this is; people are so relieved that they've solved the problem that they goof it up in the last step.
Swapping radians and degrees
Degrees are commonly used in physics problems — except when it comes to angular velocity and acceleration. That's when you have to make sure you're working with radians. If you are using a graphing calculator, make sure your calculator is set correctly in either degrees or radians before you solve the problem. You can also use the 180 degrees / ð conversion factor to convert from radians to degrees when needed.
Getting sines and cosines mixed up
Physics students often make the mistake of interchanging sines and cosines.
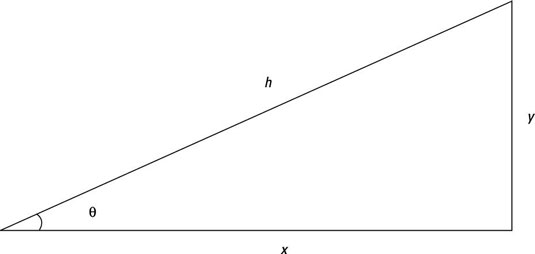
Keep the following relationships in mind:
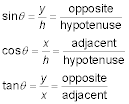
Not treating vectors as vectors
When you add vectors, use vector addition. That means resolving vectors into components. Too many people just add the magnitudes of the vectors without realizing that they should be adding components instead.
Neglecting latent heat
When you're faced with a problem that involves a phase change, such as from ice to water, don't forget to take the latent heat into account. When ice changes into water, it absorbs latent heat that you have to account for in your solution.
Getting refraction angles wrong
When you deal with refraction problems, make sure you get the angles right; they're measured with respect to a line perpendicular — called the normal — to the interface from one medium to the other. Many people incorrectly use the angle between the ray of light and the interface between the two mediums.
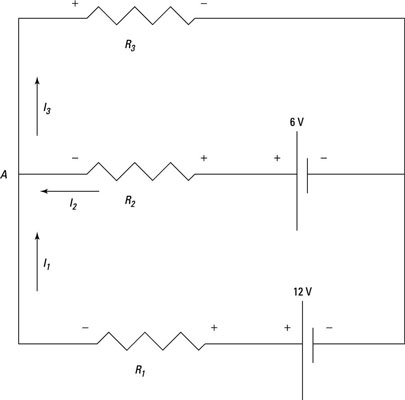
Getting the signs wrong in Kirchhoff loops
You use Kirchhoff's laws to solve for the currents in a circuit, but many people run into trouble with Kirchhoff's laws problems because they get the signs wrong.
To be sure you get the signs right, put in arrows for all the currents. Don't worry about getting the direction wrong for an arrow; if you do, the current will just come out negative. Then put a + sign where the current enters each resistor and a – sign where the current leaves each resistor.
Adding resistors incorrectly
When you have resistors in series, the current has to pass through one after the other. Here's how you calculate the total resistance of two resistors in a series:
R = R1 + R2
When you have two resistors in parallel, the current divides between the two of them, and you add the resistors, like this:
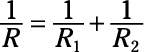
Remember, placing resistors in series increases the overall resistance. Placing resistors in parallel decreases the overall resistance. Lots of people get these two confused — make sure you don't.
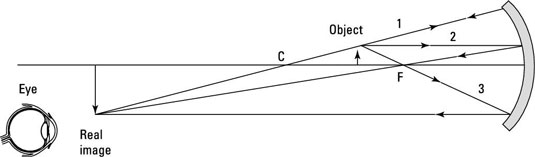
Using the wrong rays in ray diagrams
Ray diagrams are easy to get wrong because you can easily use the wrong rays.
Bear in mind these rules for ray diagrams for concave mirrors:
Ray 1: This ray goes from the object, bounces off the mirror, and goes through the center of curvature.
Ray 2: This ray goes horizontally from the object to the mirror, bounces off, and goes through the focal point.
Ray 3: This ray goes from the object through the focal point, bounces off the mirror, and ends up going parallel to the horizontal axis.
The rules for ray diagrams for convex mirrors are similar:
Ray 1: This ray goes from the object, bounces off the mirror, and goes through the center of curvature.
Ray 2: This ray goes horizontally from the object to the mirror, bounces off, and goes directly away from an imaginary focal point behind the mirror.
Ray 3: This ray goes from the object toward an imaginary focal point behind the mirror, bounces off the mirror, and ends up going parallel to the horizontal axis.
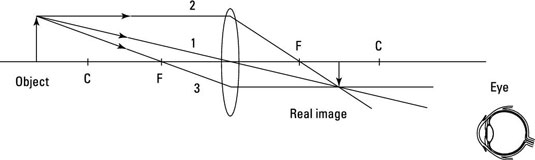
And here are the rules for ray diagrams for convex lenses:
Ray 1: This ray goes from the object straight through the center of the lens.
Ray 2: This ray goes horizontally from the object to the lens and then goes through the focal point.
Ray 3: This ray goes from the object through the focal point, through the lens, and ends up going parallel to the horizontal axis.
And finally for concave lenses:
Ray 1: This ray goes straight through the center of the lens.
Ray 2: This ray goes horizontally from the object to the lens, and then goes directly away from the focal point on the same side of the lens as the initial ray.
Ray 3: This ray goes from the object toward the focal point on the other side of the lens, and then goes parallel to the horizontal axis after the lens.