All the famous statistical significance tests (Student t, chi-square, ANOVA, and so on) work on the same general principle — they evaluate the size of apparent effect you see in your data against the size of the random fluctuations present in your data. Following are the general steps that underlie all the common statistical tests of significance.
Boil your raw data down into a single number, called a test statistic.
Each test has its own formula, but in general, the test statistic represents the magnitude of the effect you're looking for relative to the magnitude of the random noise in your data. For example, the test statistic for the unpaired Student t test for comparing means between two groups is related to the ratio:
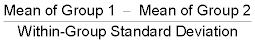
(The actual formula for the Student t statistic also includes terms involving the number of subjects in each group.) The numerator of the ratio is a measure of the effect you're looking for — the difference between the two groups. And the denominator is a measure of the random noise in your data — the spread of values within each group. The larger the observed effect is, relative to the amount of random scatter in your data, the larger the Student t statistic will be.
Determine how likely (or unlikely) it is for random fluctuations to produce a test statistic as large as the one you actually got from your data (the "p value").
The mathematicians have done the hard work; they've developed probability distribution formulas (really complicated ones) that describe how much the test statistic bounces around if only random fluctuations are present (that is, if H0 is true). Once you've calculated the test statistic, you can use the probability distribution formulas (or refer to a table of values) to obtain the p value for the test.
Interpret the "p value" and draw your conclusions.
If the p value is less than 0.05 (or some other pre-specified value), then there is very little chance (less than 1 in 20) that random fluctuations alone, in the absence of any real effect, could have produced an effect as large as what you actually observed. So you conclude that the effect you observed was statistically significant.

