Probability is the mathematics of deciding how likely an event is to occur. You can calculate the probability of an event by using the following formula:
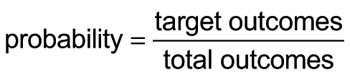
For example, when you roll a single six-sided die, you can get six total outcomes: 1, 2, 3, 4, 5, or 6. Every time you add a die, the number of total outcomes is multiplied by 6. If you roll a pair of dice, for example, the number of total outcomes is 62 = 6 × 6 = 36, meaning every roll of the dice has a total of 36 possible outcomes.
You can use the formula for probability to calculate the probability of each possible roll. For example, suppose you want to calculate the probability of rolling an 11. You can make the target outcome in one of two ways: roll a 5-6 or roll a 6-5. So, plug 2 for target outcomes and 36 for total outcomes into the formula for probability:
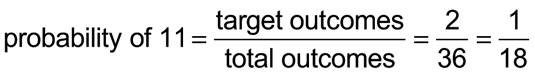
Therefore, the probability of rolling an 11 with two dice is 1/18.
Every roll of two dice has 36 total outcomes. This table shows how to calculate the probability of rolling each number with two dice.
| Roll | Target Outcomes | Probability | Roll | Target Outcomes | Probability |
|---|---|---|---|---|---|
| 2 | 1 | 1/36 | 8 | 5 | 5/36 |
| 3 | 2 | 2/36 = 1/18 | 9 | 4 | 4/36 = 1/9 |
| 4 | 3 | 3/36 = 1/12 | 10 | 3 | 3/36 = 1/12 |
| 5 | 4 | 4/36 = 1/9 | 11 | 2 | 2/26 = 1/18 |
| 6 | 5 | 5/36 | 12 | 1 | 1/36 |
| 7 | 6 | 6/36 = 1/6 |
You can use probability to figure out the odds of winning and losing in the popular casino dice game of craps. In the game of craps, on your first roll (called the come out roll), three outcomes are possible:
Natural: Rolling a total of 7 or 11 — automatically wins.
Craps: Rolling a total of 2, 3, or 12 — automatically loses.
Point: Rolling a 4, 5, 6, 8, 9, or 10 — establishes the point for the next round of rolling.

