The trig identities come in sums, differences, ratios, multiples, and halves. With a half-angle identity, you can get the value of a sine for a 15-degree angle using a function of of 30 degree angle. You can also get the value of the tangent of a 22 1/2-degree angle by using a function of an angle of 45 degrees. These identities just create more and more ways to establish an exact value for many of the more commonly used trig functions.
These half-angle identities find the function value for half the measure of angle θ:
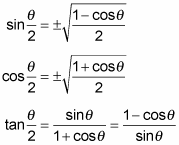
The half-angle identities are a result of taking the double-angle identities and scrunching them around. A more-technical term for scrunching is to solve for the single angle in a double-angle identity. Here’s how the half-angle identity for sine came to be:
-
Write the double-angle identity for cosine that has just a sine in it.
cos 2θ = 1 – 2sin2θ
Using the double-angle identity for cosine works better than the double-angle identity for sine, because the sine formula has both sine and cosine functions on the right side of the equation, and you can’t easily get rid of one or the other.
-
Solve for sinθ.
First, get the sin2θ term by itself on the left.
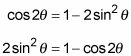
-
Divide each side by 2 and then take the square root of each side.
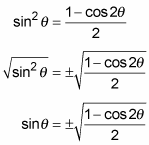
-
Replace 2θ with α and θ with α/2.
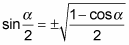
By switching the letters, you can see the relationship between the two angles, that one is half as big as the other, more easily.

