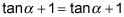With a trigonometry identity, working on both sides of the equation is even more fun than working on both sides of an algebraic equation. In algebra, you can multiply each side by the same number, square both sides, add or subtract the same thing to each side, and so on. When you solve trig identities and equations, you can use all those algebra rules plus you can do substitutions with the various trig identities when you need them. You can even insert a different identity on each side — the one big advantage of working on both sides of a trig identity.
This first example is rather basic, but it gets the idea across. Solve the identity
by working both sides.
-
Change the functions that aren’t one of the three basic functions by using their reciprocal identities.
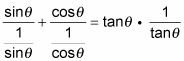
-
Simplify the two fractions on the left by flipping the denominators and multiplying them by their numerators.
Then multiply the two factors on the right together.
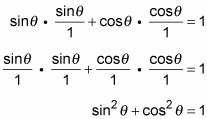
-
Replace the sum on the left by using the Pythagorean identity.
You end up with 1 = 1.
In the next example, you change everything to sines and cosines. Prove the identity
-
Change the functions to their equivalences by using the reciprocal and ratio identities.
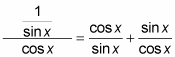
-
On the left, flip the denominator and multiply it by the numerator.
On the right, multiply each fraction by a fraction equal to 1 (by using the other fraction’s denominator) to get common denominators for all the fractions.
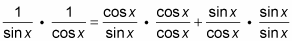
-
Simplify the multiplied fractions.
Add the two fractions on the right together.
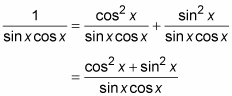
-
Replace the numerator on the right with the value from the Pythagorean identity.
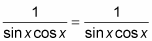
This last example requires a little creativity to get the job done. But working on both sides still works best when showing that the following is an identity:
-
Split up the fraction on the left by writing each term in the numerator over the denominator.
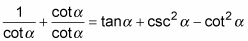
-
Reduce the second fraction to 1.
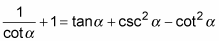
-
Replace the csc2 on the right with its equivalent by using the Pythagorean identity.
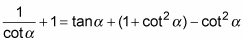
-
Simplify the terms on the right — two are opposites of one another.
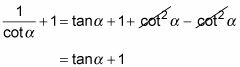
-
Replace the fraction on the left by using the reciprocal identity.