The graphs of the tangent and cotangent functions are quite interesting because they involve two horizontal asymptotes. The asymptotes help with the shapes of the curves and emphasize the fact that some angles won’t work with the functions.
The tangent and cotangent functions have restricted inputs — certain angles don’t jibe with them. But their outputs go through all the real numbers. If you switch those two groups of numbers to fit the inverses of tangent and cotangent, you can say that the inputs go through all the real numbers, and the outputs are restricted.
The two horizontal asymptotes for the inverse tangent function are
because the tangent function doesn’t exist for those two angle measures. The tangent function isn’t defined wherever the cosine is equal to 0. The graph of the inverse tangent has x-values from negative infinity to positive infinity, with all y-values between those two asymptotes.
The two horizontal asymptotes for the inverse cotangent function are y = 0 and y = π. As with the inverse tangent, the inverse cotangent function goes from negative infinity to positive infinity between the asymptotes. Check out both graphs in the following figure.
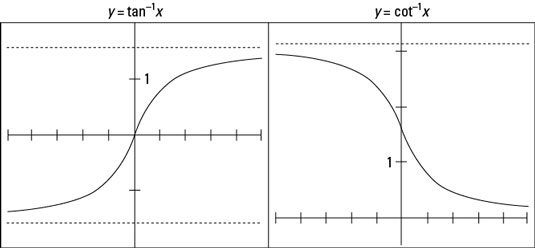
The main differences between these two graphs is that the inverse tangent curve rises as you go from left to right, and the inverse cotangent falls as you go from left to right. Also, the horizontal asymptotes for inverse tangent capture the angle measures for the first and fourth quadrants; the horizontal asymptotes for inverse cotangent capture the first and second quadrants. The measures between these asymptotes are, of course, consistent with the ranges of the two inverse functions.

