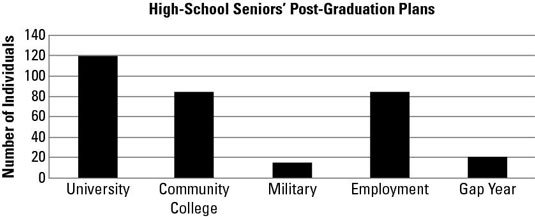
A good graph displays data in a way that's fair, makes sense, and makes a point. Not all graphs possess these qualities. The following bar chart represents the post-graduation plans of the graduating seniors from one high school. Assume that every student chose exactly one of these five options.
(Note: A gap year means that the student is taking a year off before deciding what to do.)
Sample questions
What is the most common post-graduation plan for these seniors?
Answer: Attend a university.
University is the tallest bar in the graph and therefore represents the greatest number of students of any category.
What is the least common post-graduation plan for these seniors?
Answer: Go into the military.
Military is the shortest bar in the graph and therefore represents the fewest number of students.
Assuming that each student has chosen exactly one of the five possibilities, about how many students plan to either take a gap year or attend a university?
Answer: 140
Judging by the height of the bars, about 120 students plan to attend a university, and about 20 plan to take a gap year. So 120 + 20 = 140 students.
How many total students are represented in this chart?
Answer: 322
You can find the number of students in each category from the height of the bars and then add them together: 120 + 82 + 18 + 82 + 20 = 322.
What percentage of the graduating class is planning on attending a community college?
Answer: 25%
You can find the number of students in each category from the height of the bars. The total number of students is 322 (120 + 82 + 18 + 82 + 20 = 322). The number going to a community college is 82.
To find the percentage of students going to a community college, divide the number of students in that category by the total number of students: 82/322 = 0.2546, or about 25%.
What percentage of the graduating class is not planning to attend a university?
Answer: 63%
Judging from the height of the bars, there are 322 students total (120 + 82 + 18 + 82 + 20 = 322), and 120 plan to attend a university. To find the percentage of students not planning to attend a university, subtract the number that do plan to attend from the total number of students (322 – 120 = 202), and then divide by the total: 202/322 = 0.627, or about 63%.
This bar chart displays the same information but is more difficult to interpret. Why is this the case?
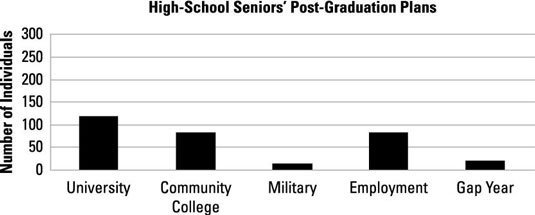
Answer: The y-axis has been stretched far beyond the range of the data.
The largest value is 120 but the y-axis runs to 300, making it difficult to compare the height of the bars.
If you need more practice on this and other topics from your statistics course, visit 1,001 Statistics Practice Problems For Dummies to purchase online access to 1,001 statistics practice problems! We can help you track your performance, see where you need to study, and create customized problem sets to master your stats skills.

