How to Identify Skew and Symmetry in a Statistical Histogram

Sometimes the mean versus median debate can get quite interesting (even beyond mathematician standards). Especially when you look at the skewness and symmetry of your statistical data in a histogram.

For example, suppose you’re part of an NBA team trying to negotiate salaries. If you represent the owners, you want to show how much everyone is making and how much money you’re spending, so you want to take into account those superstar players and report the average. But if you’re on the side of the players, you would want to report the median, because that’s more representative of what the players in the middle are making. Fifty percent of the players make a salary above the median, and 50 percent make a salary below the median.

To sort it all out, it’s best to find and compare both the mean and the median. A graph showing the shape of the data is a great place to start.

One of the graphs you can make to illustrate the shape of numerical data (how many values are close to/far from the mean, where the center is, how many outliers there might be) is a histogram.

A histogram is a graph that organizes and displays numerical data in picture form, showing groups of data and the number or percentage of the data that fall into each group. It gives you a nice snapshot of the data set.

Data sets can have many different possible shapes; here is a sampling of three shapes that are commonly discussed in introductory statistics courses:

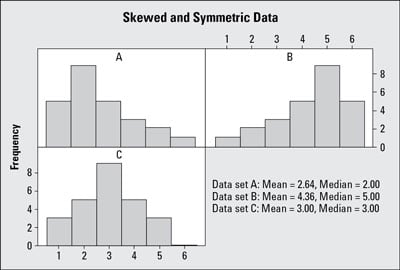
• If most of the data are on the left side of the histogram but a few larger values are on the right, the data are said to be skewed to the right.

  Histogram A in the figure shows an example of data that are skewed to the right. The few larger values bring the mean upwards but don’t really affect the median. So when data are skewed right, the mean is larger than the median. An example of such data would be NBA team salaries where star players make a lot more than their teammates.

• If most of the data are on the right, with a few smaller values showing up on the left side of the histogram, the data are skewed to the left.

  Histogram B in the figure shows an example of data that are skewed to the left. The few smaller values bring the mean down, and again the median is minimally affected (if at all). An example of skewed-left data is the amount of time students use to take an exam; some students leave early, more of them stay later, and many stay until the bitter end (some would stay forever if they could!). When data are skewed left, the mean is smaller than the median.

• If the data are symmetric, they have about the same shape on either side of the middle. In other words, if you fold the histogram in half, it looks about the same on both sides.

  Histogram C in the figure shows an example of symmetric data. With symmetric data, the mean and median are close together.

By looking at Histogram A in the figure (whose shape is skewed right), you can see that the “tail” of the graph (where the bars are getting shorter) is to the right, while the “tail” is to the left in Histogram B (whose shape is skewed left). By looking at the direction of the tail of a skewed distribution, you determine the direction of the skewness. Always add the direction when describing a skewed distribution.

Histogram C is symmetric (it has about the same shape on each side). However, not all symmetric data has a bell shape like Histogram C does. As long as the shape is approximately the same on both sides, then you say that the shape is symmetric.

Each histogram offers valuable insight into your skewed and symmetric data. In other words, you don't have to own an NBA team to find this useful!