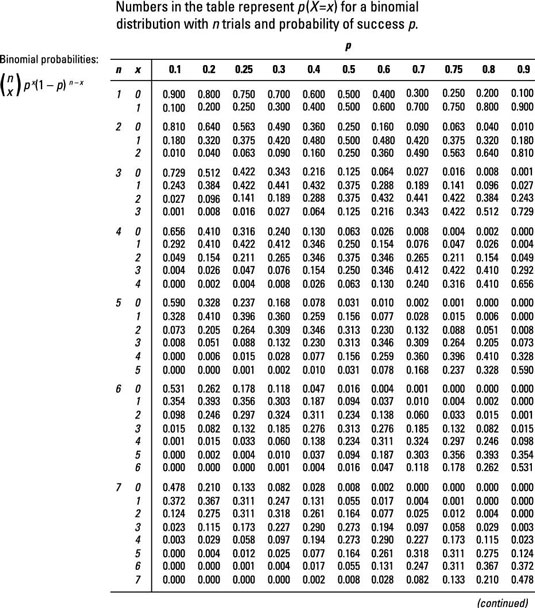
For the sample questions here, X is a random variable with a binomial distribution with n = 11 and p = 0.4. Use the binomial table to answer the following problems.



Sample questions
What is P(X = 5)?
Answer: 0.221
The binomial table has a series of mini-tables inside of it, one for each selected value of n. To find P(X = 5), where n = 11 and p = 0.4, locate the mini-table for n = 11, find the row for x = 5, and follow across to where it intersects with the column for p = 0.4. This value is 0.221.
What is P(X > 0)?
Answer: 0.996
To find the probability that X is greater than 0, find the probability that X is equal to 0, and then subtract that probability from 1. This makes the calculations much easier.
The binomial table has a series of mini-tables inside of it, one for each selected value of n. To find P(X = 0), where n = 11 and p = 0.4, locate the mini-table for n = 11, find the row for x = 0, and follow across to where it intersects with the column for p = 0.4. This value is 0.004. Now subtract that from 1:
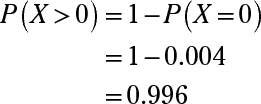
What is
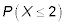
Answer: 0.120
To find the probability that X is less than or equal to 2, you first need to find the probability of each possible value of X less than 2. In other words, you find the values for P(X = 0), P(X = 1), and P(X = 2).
To find each of these probabilities, use the binomial table, which has a series of mini-tables inside of it, one for each selected value of n. To find P(X = 0), where n = 11 and p = 0.4, locate the mini-table for n = 11, find the row for x = 0, and follow across to where it intersects with the column for p = 0.4. This value is 0.004.
Now do the same for the other probabilities: P(X = 1) = 0.027 and P(X = 2) = 0.089. Finally, add these probabilities together:
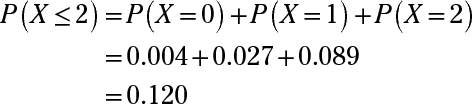
What is P(X > 9)?
Answer: 0.001
To find the probability that X is greater than 9, first find the probability that X is equal to 10 or 11 (in this case, 11 is the greatest possible value of x because there are only 11 total trials).
To find each of these probabilities, use the binomial table, which has a series of mini-tables inside of it, one for each selected value of n. To find P(X = 10), where n = 11 and p = 0.4, locate the mini-table for n = 11, find the row for x = 10, and follow across to where it intersects with the column for p = 0.4. This value is 0.001.
Now do the same for P(X = 11), which gives you 0.000. (Note: P(X = 11) isn't exactly 0.000 here; it's just a smaller probability than can be expressed in the four decimal places used in this table.) Finally, add the two probabilities together:
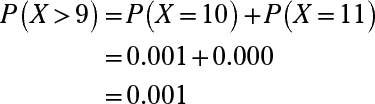
What is
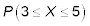
Answer: 0.634
Here, you want to find the probability equal to 3 and 5 and everything in between. In other words, you want the probabilities for X = 3, X = 4, and X = 5. You know that n = 11 and p = 0.4, which is the probability of success on each trial.
To find each of these probabilities, use the binomial table, which has a series of mini-tables inside of it, one for each selected value of n. To find P(X = 3), where n = 11 and p = 0.4, locate the mini-table for n = 11, find the row for x = 3, and follow across to where it intersects with the column for p = 0.4. This value is 0.177.
Now do the same for the other probabilities: P(X = 4) = 0.236 and P(X = 5) = 0.221. Finally, add these probabilities together:
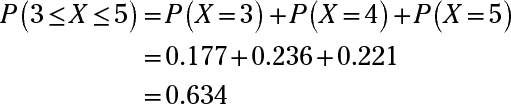
If you need more practice on this and other topics from your statistics course, visit 1,001 Statistics Practice Problems For Dummies to purchase online access to 1,001 statistics practice problems! We can help you track your performance, see where you need to study, and create customized problem sets to master your stats skills.

