Spiraling Outward
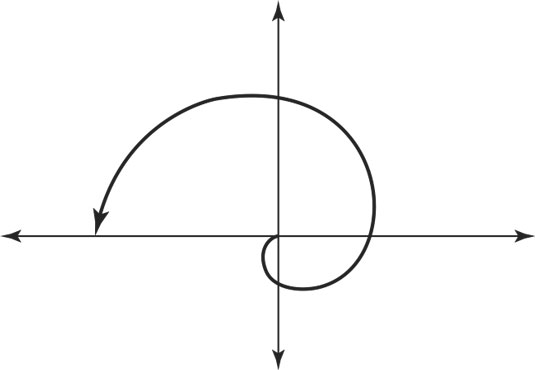
You see spirals in the ocean’s shells and the far-reaches of space. And you can create them from polar functions. The general form for a spiral is r = aθ, where θ is the angle measure in radians and a is a number multiplier. In the graph of r = 1/3θ. The 1/3 multiplier makes the spiral tighter around the pole. A larger number will make it spread out farther more quickly. And what about a negative number multiplier? It makes the spiral move out in the opposite direction — clockwise instead of counterclockwise. The figure shows you an example of just such a spiral.
Falling in Love with a Cardioid
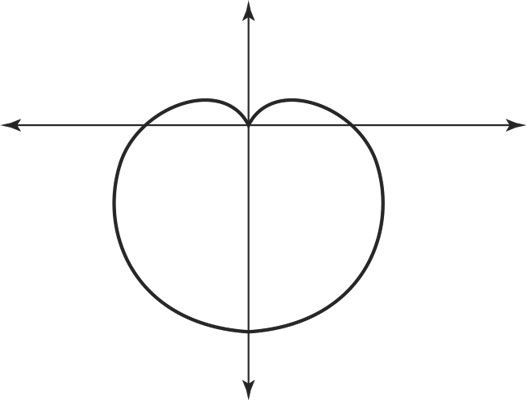
The graph of a cardioid can resemble an apple without a stem. But its name actually comes from the Greek word for heart. This curve is the trace of a point on the perimeter of one circle that’s rolling around another circle. Because that type of trace is hard to do, plugging the equation into a graphing mechanism is much easier. The general forms of the cardioid curve are
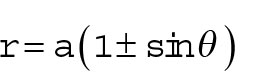
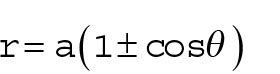
When the sine is used and when θ is a negative angle, then you get Newton’s favorite fruit, as seen in the figure.
Cardioids and Lima Beans
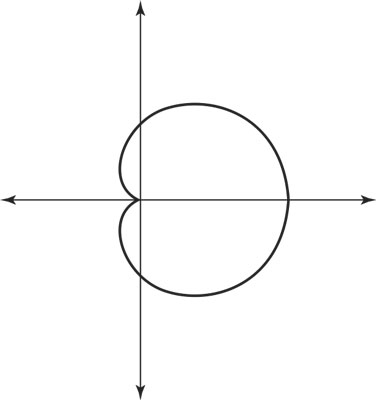
A cardioid can face left or right when the cosine is used in the function definition. The left-facing lima bean in this graph comes from a function where the input θ involves only positive measures of angles: r = 2(1 + cosθ).
Leaning Lemniscates
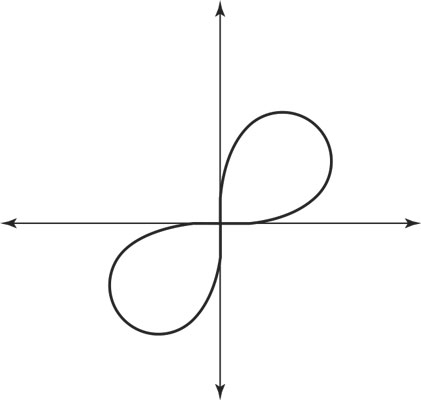
A lemniscate resembles the symbol for infinity. Its name comes from the Latin, meaning “decorated with ribbons.” This curve can either cut diagonally through the quadrants or lie on the axes and be speared through like a shish kabob. A lemniscate with a sine in its function does the diagonal cut. The general format of the equation for such a curve is
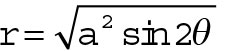
Increasing the size of the multiplier a increases the length of the petals. You see the lemniscate
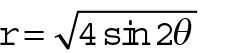
Lacing through Lemniscates
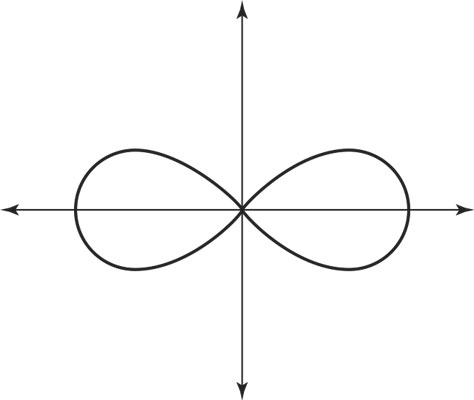
Lemniscates that are skewered by the axes have an equation in the general form of
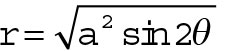
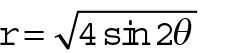
Roses with Even Petals
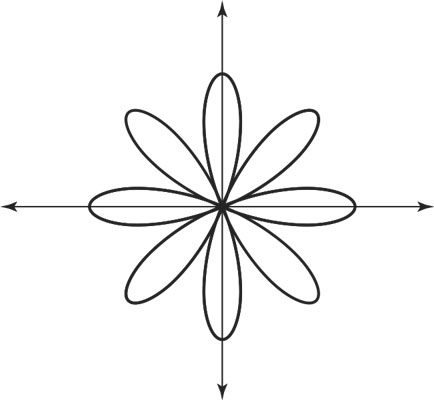
Roses also can be represented using sine or cosine. The number of petals is determined by whether the angle’s multiplier is even or odd. Using the cosine in the general format, the rose has an equation r = acosbθ. If b is even, then there are 2b petals. So, the rose drawn from r = 2cos4θ has eight petals, as shown.
A Rose Is a Rose Is a Rose
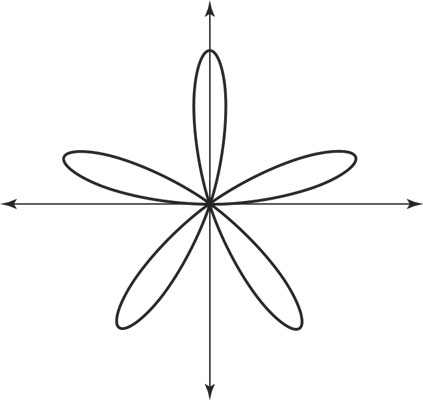
Writing the function equation for a rose using the sine, you have r = asinbθ. When b is an odd number, the number of petals is b. The rose shown in the figure has five petals, and its function equation is r = 2sin5θ.
Limaçon or Escargot?
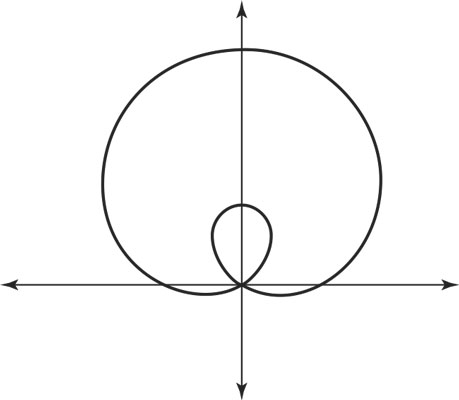
A limaçon can sometimes resemble a cardioid and even look like an oval. But it’s the unique curve-within-a-curve versions that make it so elegant. The word limaçon comes from the French, meaning “snail.” Using the general form r = a ± bsinθ, you have a curve sitting on top of the pole, rather than on the side. If you let a < b, then the second curve appears inside the first, as shown here with r = 1 + 2sinθ.
Limaçon on the Side
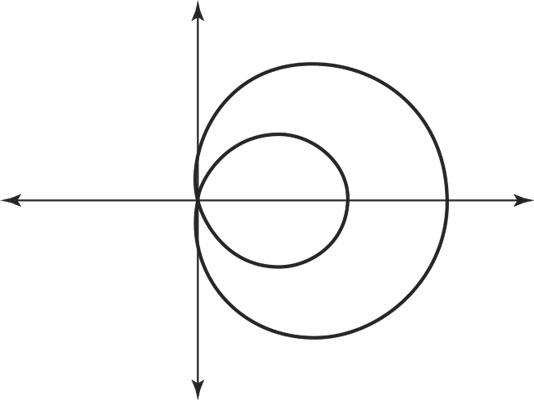
Limaçon curves can change their position about the pole — mainly due to which function is being used. Increasing the difference between a and b in the general equation r = a ± bcosθ can also change the curves, as you see in the sketch of r = 1 + 4cosθ in the figure.
Bifolium or Rabbit Ears?
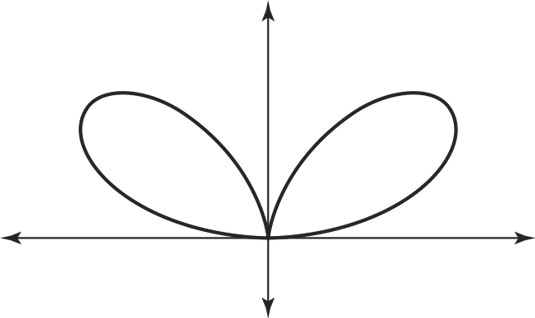
And, just when you thought there’d be no more ways to change things up with these curves, I finish with the bifolium. With the “bi” in its name, you already have a hint as to what you’ll find. The general equation r = asinθcos2θ is a bit unique, because both sine and cosine appear in its function equation. The symmetry is different in this curve — a reflection rather than rotation. (See the figure.)

